
 已知矩形ABCD的边BC=2AB,E是BC中点,F在DC上,∠FAC=∠EAC.求DF:DC的比值.
已知矩形ABCD的边BC=2AB,E是BC中点,F在DC上,∠FAC=∠EAC.求DF:DC的比值. 分析 作EM⊥AC于M,作FN⊥AC于N,设EM=a,FN=b,先求出CM=2a,CE=BE=AB=$\sqrt{5}$a,再根据勾股定理求出AC=5a,然后求出FN=2b,CF=$\sqrt{5}$b,由∠FAC=∠EAC,得出tan∠FAC=$\frac{DN}{AN}$=tan∠EAC,得出$\frac{2b}{5a-b}$=$\frac{1}{3}$,b=$\frac{5}{7}$a,求出CF、DF,即可求出DF:DC的值.
解答 解:作EM⊥AC于M,作FN⊥AC于N,如图所示: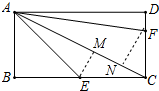 则∠AME=∠CME=90°,∠ANF=∠CNF=90°,
则∠AME=∠CME=90°,∠ANF=∠CNF=90°,
设EM=a,CN=b,
∵四边形ABCD是矩形,
∴∠B=∠BCD=90°,
∵BC=2AB,
∴tan∠ACB=$\frac{EM}{CM}$=$\frac{AB}{BC}$=$\frac{1}{2}$,
∴CM=2EM=2a,
∴CE=$\sqrt{5}$a,
∵E是BC的中点,
∴AB=BE=CE=$\sqrt{5}$a,
∴AC=$\sqrt{(\sqrt{5})^{2}+(2\sqrt{5})^{2}}$a=5a,
∴AM=3a,
∵cot∠FCN=$\frac{CN}{FN}$=tan∠ACB=$\frac{1}{2}$,
∴FN=2b,
∴CF=$\sqrt{5}$b,
∵∠FAC=∠EAC,
∴tan∠FAC=$\frac{FN}{AN}$=tan∠EAC=$\frac{a}{3a}$=$\frac{1}{3}$,
∴$\frac{2b}{5a-b}$=$\frac{1}{3}$,
∴b=$\frac{5}{7}$a,
∴CF=$\frac{5\sqrt{5}a}{7}$,
∴DF=CD-CF=$\sqrt{5}$a-$\frac{5\sqrt{5}a}{7}$=$\frac{2\sqrt{5}a}{7}$,
∴DF:DC=$\frac{2\sqrt{5}a}{7}$:$\sqrt{5}$a=$\frac{2}{7}$.
点评 本题考查了矩形的性质、勾股定理、锐角三角函数等知识;本题难度较大,需要通过作辅助线设出未知数才能得出结果.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
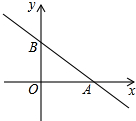 如图,一次函数y=kx+b的图象交y轴于点B(0,3),与x轴正半轴交于点A,cos∠BAO=$\frac{4}{5}$
如图,一次函数y=kx+b的图象交y轴于点B(0,3),与x轴正半轴交于点A,cos∠BAO=$\frac{4}{5}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com