
【题目】如图1,点A在x轴上,OA=4,将OA绕点O逆时针旋转120°至OB的位置.
(1)求经过A、O、B三点的抛物线的函数解析式;
(2)在此抛物线的对称轴上是否存在点P使得以P、O、B三点为顶点的三角形是等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3 )如图2,OC=4,⊙A的半径为2,点M是⊙A上的一个动点,求MC+![]() OM的最小值.
OM的最小值.
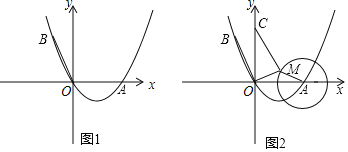
【答案】(1)y=![]() x2﹣
x2﹣![]() x;(2)存在△POB为等腰三角形,符合条件的点P只有一个,坐标为(2,2
x;(2)存在△POB为等腰三角形,符合条件的点P只有一个,坐标为(2,2![]() );(3)MC+
);(3)MC+![]() OM的最小值为CK=5.
OM的最小值为CK=5.
【解析】
(1)设出抛物线解析式,利用待定系数法求出拋物线解析式即可
(2)设点P的坐标为(2,y),分三种情况讨论,①OB=OP,②2OB=PB,③OP=PB,分别求出y的值,即可得出点P的坐
(3)在OA上取点K,使AK=1,连接CK交圆与点M,连接OM、CM ,利用△AKM∽△AMO ,求出MC+![]() OM=MC+KM=CK,即可解答
OM=MC+KM=CK,即可解答
(1)如图1,过点B作BD⊥x轴于点D,
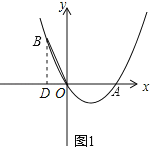
∴∠BDO=90°,
∵OA绕点O逆时针旋转120°至OB,
∴OB=OA=4,∠AOB=120°,B在第二象限,
∴∠BOD=60°,
∴sin∠BOD=![]() ,cos∠BOD=
,cos∠BOD=![]() ,
,
∴BD=![]() OB=2
OB=2![]() ,OD=
,OD=![]() OB=2,
OB=2,
∴B(﹣2,2![]() ),
),
设过点A(4,0),B(﹣2,2![]() ),O(0,0)的抛物线解析式为y=ax2+bx+c,
),O(0,0)的抛物线解析式为y=ax2+bx+c,
∴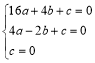 解得:
解得: ,
,
∴抛物线的函数解析式为y=![]() x2﹣
x2﹣![]() x;
x;
(2)存在△POB为等腰三角形,
∵抛物线与x轴交点为A(4,0),O(0,0),
∴对称轴为直线x=2,
设点P坐标为(2,p),
则OP2=22+p2=4+p2,BP2=(2+2)2+(p﹣2![]() )2=p2﹣4
)2=p2﹣4![]() p+28,
p+28,
①若OP=OB=4,则4+p2=42
解得:p1=2![]() ,p2=﹣2
,p2=﹣2![]() ,
,
当p=﹣2![]() 时,∠POA=60°,即点P、O、B在同一直线上,
时,∠POA=60°,即点P、O、B在同一直线上,
∴p≠﹣2![]() ,
,
∴P(2,2![]() ),
),
②若BP=OB=4,则p2﹣4![]() p+28=42
p+28=42
解得:p1=p2=2![]() ,
,
∴P(2,2![]() );
);
③若OP=BP,则4+p2=p2﹣4![]() p+28,
p+28,
解得:p=2![]() ,
,
∴P(2,2![]() );
);
综上所述,符合条件的点P只有一个,坐标为(2,2![]() );
);
(3)在OA上取点K,使AK=1,连接CK交圆与点M,连接OM、CM,
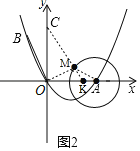
此时,MC+![]() OM=MC+KM=CK为最小值,
OM=MC+KM=CK为最小值,
理由:∵AK=1,MA=2,OA=4,
∴AM2=AKOA
∴△AKM∽△AMO,∴![]() =
=![]() ,
,
即:MC+![]() OM=MC+KM=CK,
OM=MC+KM=CK,
CK=![]() =5,
=5,
即:MC+![]() OM的最小值为CK=5.
OM的最小值为CK=5.


科目:初中数学 来源: 题型:
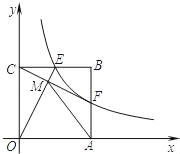
【题目】如图,点B的坐标是(4,4),作BA⊥x轴于点A,作BC⊥y轴于点C,反比例函数![]() (k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,OE与CF交于点M,连接AM.
(k>0)的图象经过BC的中点E,与AB交于点F,分别连接OE、CF,OE与CF交于点M,连接AM.
(1)求反比例函数的函数解析式及点F的坐标;
(2)你认为线段OE与CF有何位置关系?请说明你的理由.
(3)求证:AM=AO.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形![]() 的
的![]() ,
,![]() 边上分别任取一点
边上分别任取一点![]() ,
,![]() ,且
,且![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() .下列四个结论:①若
.下列四个结论:①若![]() ,则
,则![]() ;②若
;②若![]() ,
,![]() ,则
,则![]() ;③
;③![]() ;④若
;④若![]() ,则
,则![]() 的最小值为
的最小值为![]() ,其中正确的是( )
,其中正确的是( )
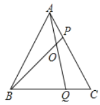
A.①②④B.①③④C.②③④D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(4分)一元二次方程![]() 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
【答案】A.
【解析】
试题∵△=![]() ,∴方程有两个不相等的实数根.故选A.
,∴方程有两个不相等的实数根.故选A.
考点:根的判别式.
【题型】单选题
【结束】
9
【题目】已知直线y=kx(k>0)与双曲线![]() 交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
交于点A(x1,y1),B(x2,y2)两点,则x1y2+x2y1的值为【 】
A.﹣6 B.﹣9 C.0 D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
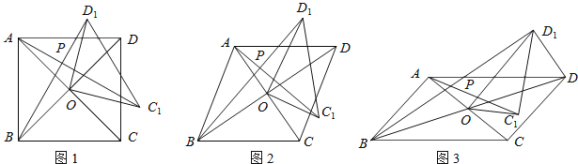
【题目】在四边形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转得到
按逆时针方向旋转得到![]() ,旋转角为θ(0°<θ<90°),连接
,旋转角为θ(0°<θ<90°),连接![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)如图1,若四边形![]() 是正方形.
是正方形.
①求证:![]() ≌
≌![]() .
.
②请直接写出![]() 与
与![]() 的位置关系.
的位置关系.
(2)如图2,若四边形![]() 是菱形,
是菱形,![]() ,
,![]() ,设
,设![]() .判断
.判断![]() 与
与![]() 的位置关系,说明理由,并求出
的位置关系,说明理由,并求出![]() 的值.
的值.
(3)如图3,若四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,连接
,连接![]() ,设
,设![]() .请直接写出
.请直接写出![]() 的值和
的值和![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
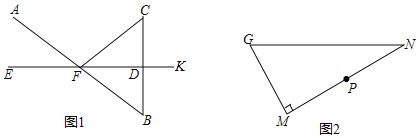
【题目】(1)如图1,已知EK垂直平分BC,垂足为D,AB与EK相交于点F,连接CF.求证:∠AFE=∠CFD.
(2)如图2,在Rt△GMN中,∠M=90°,P为MN的中点.
①用直尺和圆规在GN边上求作点Q,使得∠GQM=∠PQN(保留作图痕迹,不要求写作法);
②在①的条件下,如果∠G=60°,那么Q是GN的中点吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级6个班的180名学生即将参加北京市中学生开放性科学实践活动送课到校课程的学习.学习内容包括以下7个领域:A.自然与环境,B.健康与安全,C.结构与机械,D.电子与控制,E.数据与信息,F.能源与材料,G.人文与历史.为了解学生喜欢的课程领域,学生会开展了一次调查研究,请将下面的过程补全.
收集数据学生会计划调查30名学生喜欢的课程领域作为样本,下面抽样调查的对象选择合理的是 ;(填序号)
①选择七年级1班、2班各15名学生作为调查对象
②选择机器人社团的30名学生作为调查对象
③选择各班学号为6的倍数的30名学生作为调查对象
调查对象确定后,调查小组获得了30名学生喜欢的课程领域如下:
A,C,D,D,G,G,F,E,B,G,
C,C,G,D,B,A,G,F,F,A,
G,B,F,G,E,G,A,B,G,G
整理、描述数据整理、描述样本数据,绘制统计图表如下,请补全统计表和统计图.
某校七年级学生喜欢的课程领域统计表
课程领域 | 人数 |
A | 4 |
B | 4 |
C | 3 |
D | 3 |
E | 2 |
F | 4 |
G | 10 |
合计 | 30 |
分析数据、推断结论请你根据上述调查结果向学校推荐本次送课到校的课程领域,你的推荐是 (填A﹣G的字母代号),估计全年级大约有 名学生喜欢这个课程领域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元,到2018年盈利2160万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,那么2019年该公司盈利能否达到2500万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com