Question

4．探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？
如图甲，∠FDC、∠ECD为△ADC的两个外角，则∠A与∠FDC+∠ECD的数量关系∠FDC+∠ECD=180°+∠A．
探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？
如图乙，在△ADC中，DP、CP分别平分∠ADC和∠ACD，则∠P与∠A的数量关系∠P=90°+$\frac{1}{2}$∠A．
探究三：若将△ADC改为任意四边形ABCD呢？
已知：如图丙，在四边形ABCD中，DP、CP分别平分∠ADC和∠BCD，则∠P与∠A+∠B的数量关系∠P=$\frac{1}{2}$（∠A+∠B）．
探究四：若将上题中的四边形ABCD改为六边形ABCDEF呢？如图丁
则∠P与∠A+∠B+∠E+∠F的数量关系∠P=$\frac{1}{2}$（∠A+∠B+∠E+∠F）-180°．

探究五：如图，四边形ABCD中，∠F为四边形ABCD的∠ABC的角平分线及外角∠DCE的平分线所在的直线构成的锐角，若设∠A=α，∠D=β；
（1）如图①，α+β＞180°，则∠F=∠F=$\frac{1}{2}$（α+β）-90°；（用α，β表示）
（2）如图②，α+β＜180°，请在图中画出∠F，且∠F=∠F=90°-$\frac{1}{2}$（α+β）；（用α，β表示）
（3）一定存在∠F吗？如有，直接写出∠F的值，如不一定，直接指出α，β满足什么条件时，不存在∠F．

Answer 1

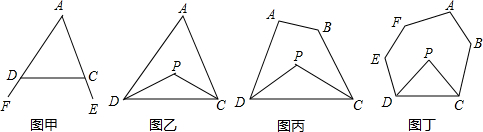
分析 探究一：根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD，∠ECD=∠A+∠ADC，再根据三角形内角和定理整理即可得解；
探究二：根据角平分线的定义可得∠PDC=$\frac{1}{2}$∠ADC，∠PCD=$\frac{1}{2}$∠ACD，然后根据三角形内角和定理列式整理即可得解；
探究三：根据四边形的内角和定理表示出∠ADC+∠BCD，然后同理探究二解答即可；
探究四：根据六边形的内角和公式表示出∠EDC+∠BCD，然后同理探究二解答即可；
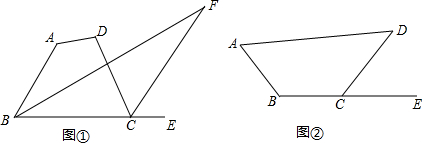
探究五：①根据四边形的内角和定理表示出∠BCD，再表示出∠DCE，然后根据角平分线的定义可得∠FBC=$\frac{1}{2}$∠ABC，∠FCE=$\frac{1}{2}$∠DCE，三角形的一个外角等于与它不相邻的两个内角的和可得∠F+∠FBC=∠FCE，然后整理即可得解；
②同①的思路求解即可；
③根据∠F的表示，∠F为0时不存在．

解答 解：探究一：∵∠FDC=∠A+∠ACD，∠ECD=∠A+∠ADC，
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A；

探究二：∵DP、CP分别平分∠ADC和∠ACD，
∴∠PDC=$\frac{1}{2}$∠ADC，∠PCD=$\frac{1}{2}$∠ACD，
∴∠DPC=180°-∠PDC-∠PCD
=180°-$\frac{1}{2}$∠ADC-$\frac{1}{2}$∠ACD
=180°-$\frac{1}{2}$（∠ADC+∠ACD）
=180°-$\frac{1}{2}$（180°-∠A）
=90°+$\frac{1}{2}$∠A；

探究三：∵DP、CP分别平分∠ADC和∠BCD，
∴∠PDC=$\frac{1}{2}$∠ADC，∠PCD=$\frac{1}{2}$∠BCD，
∴∠DPC=180°-∠PDC-∠PCD
=180°-$\frac{1}{2}$∠ADC-$\frac{1}{2}$∠BCD
=180°-$\frac{1}{2}$（∠ADC+∠BCD）
=180°-$\frac{1}{2}$（360°-∠A-∠B）
=$\frac{1}{2}$（∠A+∠B）；

探究四：六边形ABCDEF的内角和为：（6-2）•180°=720°，
∵DP、CP分别平分∠EDC和∠BCD，
∴∠PDC=$\frac{1}{2}$∠EDC，∠PCD=$\frac{1}{2}$∠BCD，
∴∠P=180°-∠PDC-∠PCD
=180°-$\frac{1}{2}$∠EDC-$\frac{1}{2}$∠BCD
=180°-$\frac{1}{2}$（∠EDC+∠BCD）
=180°-$\frac{1}{2}$（720°-∠A-∠B-∠E-∠F）
=$\frac{1}{2}$（∠A+∠B+∠E+∠F）-180°
即∠P=$\frac{1}{2}$（∠A+∠B+∠E+∠F）-180°．

探究五：①由四边形内角和定理得，∠BCD=360°-∠A-∠D-∠ABC，
∴∠DCE=180°-（360°-∠A-∠D-∠ABC）=∠A+∠D+∠ABC-180°，
由三角形的外角性质得，∠DCE=∠A+∠D+∠ABC，∠FCE=∠F+∠FBC，
∵BF、CF分别是∠ABC和∠DCE的平分线，
∴∠FBC=$\frac{1}{2}$∠ABC，∠FCE=$\frac{1}{2}$∠DCE，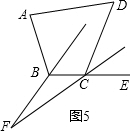
∴∠F+∠FBC=$\frac{1}{2}$（∠A+∠D+∠ABC-180°）=$\frac{1}{2}$（∠A+∠D）+$\frac{1}{2}$∠ABC-90°，
∴∠F=$\frac{1}{2}$（∠A+∠D）-90°，
∵∠A=α，∠D=β，
∴∠F=$\frac{1}{2}$（α+β）-90°；
②如图5，同①可求，∠F=90°-$\frac{1}{2}$（α+β）；
③∠F不一定存在，当α+β=180°时，∠F=0，不存在．
故答案为：探究一：∠FDC+∠ECD=180°+∠A；探究二：∠P=90°+$\frac{1}{2}$∠A；探究三：∠P=$\frac{1}{2}$（∠A+∠B）．探究四：∠P=$\frac{1}{2}$（∠A+∠B+∠E+∠F）-180°；探究五：①$∠F=\frac{1}{2}（α+β）-{90°}$，②$∠F={90°}-\frac{1}{2}（α+β）$．

点评 本题考查了三角形的外角性质，三角形的内角和定理，多边形的内角和公式，此类题目根据同一个解答思路求解是解题的关键．