Question

20．已知抛物线y=ax²-2ax-3a交x轴于A、B两点（A左B右），交y轴于点C，点D在抛物线上，CD∥x轴，将射线AD沿x轴翻折后交抛物线于点E．
（1）如图1，求线段AB的长；
（2）如图2，若AE=AD+2$\sqrt{2}$，求抛物线解析式；
（3）在（2）的条件下，延长EA交直线CD于点M，点P为第四象限内抛物线上一点，直线AP交直线CD于点N，当S_△PMN=S_△DAN时，求点P的坐标．

Answer 1

分析 （1）令y=0，求出点A，B的坐标，从而求出AB的长；
（2）先用三角函数tan∠EAG=$\frac{EG}{AG}$=$\frac{a（m+1）（m-3）}{m+1}$=a（m-3），tan∠ADG=$\frac{AF}{DF}$=$\frac{3a}{3}$=a，由∠FDA=∠BAD=∠EAG，建立方程a（m-3）=a，求出m；
（3）先求出PK=$\frac{\sqrt{2}}{2}$，PH=$\frac{\sqrt{2}}{2}$ （-t²+3t+4），从而得出S_△DAM=9，再分两种情况进行计算．

解答 解：（1）当y=0时，x²-2x-3=0，
解得：x₁=-1，x₂=3，
∴A（-1，0）B（3，0），
∴AB=4，
（2）如图1，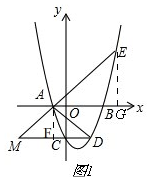

过A作AF⊥直线CD于点F，过E作EG⊥直线x轴于点G，
∴对称轴为直线x=1，
∵CD∥x轴，
∴D（2，-3a），
∴DF=3，
设E[m，a（m+1）（m-3）]，
tan∠EAG=$\frac{EG}{AG}$=$\frac{a（m+1）（m-3）}{m+1}$=a（m-3），
tan∠ADF=$\frac{AF}{DF}$=$\frac{3a}{3}$=a，
∵∠FDA=∠BAD=∠EAG，
∴a（m-3）=a，
∴m=4，
∴AG=5，
∴3AE=5AD，
∵AE=AD+2$\sqrt{2}$，
∴AD=3$\sqrt{2}$，
∴AF=3=3a，
∴a=1，
∴抛物线解析式为y=x²-2x-3；
（3）如图2，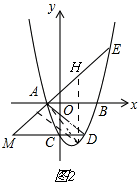

过P作PH⊥X轴交AE于点H，过P作PK⊥直线AE于点E，
∴直线AE的解析式为y=x+1，
设P（t，t²-2t-3），
则PH=t+1-（ t²-2t-3）=-t²+3t+4，
由（2）EG=AG=5，
∴∠AEG=45°=∠KHP，
∴PK=$\frac{\sqrt{2}}{2}$，PH=$\frac{\sqrt{2}}{2}$ （-t²+3t+4），
∵△AMD为等腰直角三角形，
∴AM=AD=3$\sqrt{2}$，
∴S_△DAM=9，
情况一：当P₁在CD下方时，
∵S_△PMN=S_△DAN，
∴S_△PMA=S_△DAM，
∴AM×P₁K=18，
∴$\frac{\sqrt{2}}{2}$ （-t²+3t+4）×3$\sqrt{2}$=18，
 解得t₁=1，t₂=2（舍），
∴P（1，-4）；
情况二：当P₂在CD上方时，同同情况一可得
∴S_△PMA=S_△DAM，
∴t₃=1，t₄=2（舍）
∴满足条件的点P为P（1，-4）．

点评 此题是二次函数综合题，主要考查了求坐标交点坐标，三角形的面积的计算方法，锐角三角函数的意义，解本题的关键是用三角函数值相等建立方程．