
【题目】如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣![]() x+
x+![]() 与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
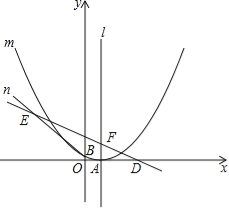
(1)求抛物线m的解析式;
(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;
(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+1;(2)点P坐标为(3,
x+1;(2)点P坐标为(3,![]() );(3)点Q坐标为(9,4)或(15,16).
);(3)点Q坐标为(9,4)或(15,16).
【解析】试题分析:(1)抛物线顶点在x轴上则可得出顶点纵坐标为0,将解析式进行配方就可以求出a的值,继而得出函数解析式;(2)作出B点关于l的对称点B′,连接EB′交l于点P,如图所示,,三角形BEP为顶点的三角形的周长最小,再求出直线B′E的解析式,进而得出P点坐标;(3)先求出直线FD的解析式,结合以线段FQ为直径的圆恰好经过点D这个条件,明确∠FDG=90°,得出直线DG解析式的k值与直线FD解析式的k值乘积为﹣1,利用D点坐标求出直线DG解析式,将点Q坐标用抛物线解析式表示后代入DG直线解析式可求出点Q坐标.
试题解析:(1)∵抛物线y=ax2﹣6ax+c(a>0)的顶点A在x轴上
∴配方得y=a(x﹣3)2﹣9a+1,则有﹣9a+1=0,解得a=![]()
∴A点坐标为(3,0),抛物线m的解析式为y=![]() x2﹣
x2﹣![]() x+1;
x+1;
(2)∵点B关于对称轴直线x=3的对称点B′为(6,1)
∴连接EB′交l于点P,如图所示

设直线EB′的解析式为y=kx+b,把(﹣7,7)(6,1)代入得
![]() 解得
解得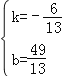 ,
,
则函数解析式为y=﹣![]() x+
x+![]()
把x=3代入解得y=![]() ,
,
∴点P坐标为(3,![]() );
);
(3)∵y=﹣![]() x+
x+![]() 与x轴交于点D,
与x轴交于点D,
∴点D坐标为(7,0),
∵y=﹣![]() x+
x+![]() 与抛物线m的对称轴l交于点F,
与抛物线m的对称轴l交于点F,
∴点F坐标为(3,2),
求得FD的直线解析式为y=﹣![]() x+
x+![]() ,若以FQ为直径的圆经过点D,可得∠FDQ=90°,则DQ的直线解析式的k值为2,
,若以FQ为直径的圆经过点D,可得∠FDQ=90°,则DQ的直线解析式的k值为2,
设DQ的直线解析式为y=2x+b,把(7,0)代入解得b=﹣14,则DQ的直线解析式为y=2x﹣14,
设点Q的坐标为(a,![]() ),把点Q代入y=2x﹣14得
),把点Q代入y=2x﹣14得
![]() =2a﹣14
=2a﹣14
解得a1=9,a2=15.
∴点Q坐标为(9,4)或(15,16).


科目:初中数学 来源: 题型:
【题目】如图,O为坐标原点,四边形OACB是菱形,OB在x轴的正半轴上,sin∠AOB=![]() ,反比例函数y=
,反比例函数y=![]() 在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
在第一象限内的图象经过点A,与BC交于点F,则△AOF的面积等于( )
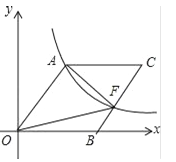
A. 60 B. 80 C. 30 D. 40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式的计算结果与x2m+2不相等的是( )
A. x2m·x2 B. xm-1·xm+3 C. x1-m·x3m+1 D. xm+2·x2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据统计,2017年河南省的夏粮收购总产量为796.24亿斤,请用科学记数法表示这个数为( )
A. 7.9624×1010 B. 7.9624×109 C. 79.624×109 D. 0.79624×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a与b互为相反数且都不为零,n为正整数,则下列两数互为相反数的是( )
A. a2n-1与-b2n-1 B. a2n-1与b2n-1 C. a2n与b2n D. an与bn
查看答案和解析>>
科目:初中数学 来源: 题型:
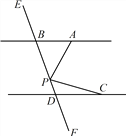
【题目】如图,已知直线AB//CD,直线EF和直线AB,CD分别交于点B和点D,在直线 EF 上有一动点P.
(1).P点在线段BD上(点P 与点B,D不重合),请证明 :∠PAB+∠PCD=∠APC;
(2).若点P不在线段BD 上,请写出∠PAB, ∠PCD, ∠APC之间的数量关系,并画出相关图形,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
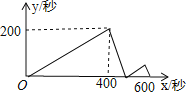
【题目】甲、乙两人在同一直线道路上同起点、同方向、同时出发,分别以不同的速度匀速跑步1500米,当甲超出乙200米时,甲停下来等候乙,甲、乙会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息,在跑步的整个过程中,甲、乙两人的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则甲到终点时,乙跑了 ______米.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com