
【题目】某商场服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,扩大销售量,增加盈利,尽量减少库存.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.假设商场降价![]() 元,
元,
(1)降价![]() 元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含
元后,每一件童装的利润为___________(元),每天可以卖出去的童装件数为____________(件)(用含![]() 的代数式表示);
的代数式表示);
(2)若销售该童装每天盈利要达到1200元,则每件童装应该降价多少元?
【答案】(1)40-![]() ,20+
,20+![]() ;(2)20
;(2)20
【解析】
(1)根据“利润=售价-进价”和“每件童装降价1元,那么平均每天就可多售出2件”,可得到结果;
(2)根据利润=销售量×单件利润列出方程即可求解;
(1)根据题意可知:原来每天可售出20件,每件盈利40元,当降价![]() 元后,每件盈利变为(40-
元后,每件盈利变为(40-![]() )元,又因为每件童装降价1元,那么平均每天就可多售出2件,降价后的销售数量为(20+
)元,又因为每件童装降价1元,那么平均每天就可多售出2件,降价后的销售数量为(20+![]() )件.
)件.
(2)由于每天总盈利利润=每天销售量×单件利润,根据(1)中的数据可列方程:
![]() ,
,
整理得:![]() ,
,
解方程得:![]() 或
或![]() ,
,
∵题目要求尽量减少库存,当![]() 时,卖出的多,库存比
时,卖出的多,库存比![]() 少,
少,
∴要使每天盈利要达到1200元,则每件童装应该降价20元


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0,②3a+c<0,③a﹣b+c>0,④4a+2b+c>0,⑤若点(﹣2,y1)和(﹣![]() ,y2)在该图象上,则y1>y2,其中正确的结论是 .(填入正确结论的序号)
,y2)在该图象上,则y1>y2,其中正确的结论是 .(填入正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
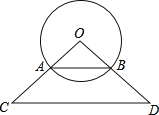
【题目】已知⊙O的半径为12cm,弦AB=12![]() cm.
cm.
(1)求圆心O到弦AB的距离.
(2)若弦AB恰好是△OCD的中位线,以CD中点E为圆点,R为半径作⊙E,当⊙O和⊙E相切时,求R的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
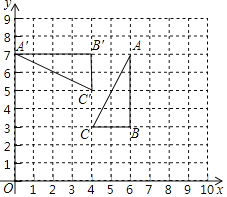
【题目】如图,在平面直角坐标系中,△ABC和△A'B'C'的顶点都在格点上.
(1)将△ABC绕点B顺时针旋转90°后得到△A1BC1;
(2)若△A'B'C'是由△ABC绕某一点旋转某一角度得到,则旋转中心的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B在数轴上分别表示数a,b.若A、B两点间的距离记为d,则d和a,b之间的数量关系是d=|a-b|.
(1)数轴上有理数x与有理数-2所对应两点之间的距离可以表示为______;
(2)|x+6|可以表示数轴上有理数x与有理数_______所对应的两点之间的距离;
若|x+6|= |x -2|,则x=______;
(3)若a=1,b=-2,将数轴折叠,使得A点与﹣7表示的点重合,则B点与数______表示的点P重合;
(4)若数轴上M、N两点之间的距离为11(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M:_____, N:_______;
(5)在题(3)的条件下,点A为定点,点B、P为动点,若移动点B、P中一点后,能否使相邻两点间距离相等?若能,请写出移动方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙、丙、丁、戊五名同学有以下说法:甲说:“直线BC不过点A”;乙说:“点A在直线CD外”; 丙说:“D在线段CB的反向延长线上;”丁说:“A,B,C,D两两连结,有5条线段” ; 戊说:“射线AD与射线CD不相交”. 其中说明正确的有( ).

A. 3人B. 4人C. 5人D. 2人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习完《有理数》后,小奇对运算产生了浓厚的兴趣.借助有理数的运算,定义了一种新运算“⊕”,规则如下:a⊕b=a×b+2×a.
(1)求2⊕(﹣1)的值;
(2)求﹣3⊕(﹣4⊕![]() )的值;
)的值;
(3)试用学习有理数的经验和方法来探究这种新运算“⊕”是否具有交换律?请写出你的探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A是抛物线![]() 与x轴正半轴的交点,点B在抛物线上,其横坐标为2,直线AB与y轴交于点
与x轴正半轴的交点,点B在抛物线上,其横坐标为2,直线AB与y轴交于点![]() 点M、P在线段AC上
点M、P在线段AC上![]() 不含端点
不含端点![]() ,点Q在抛物线上,且MQ平行于x轴,PQ平行于y轴
,点Q在抛物线上,且MQ平行于x轴,PQ平行于y轴![]() 设点P横坐标为m.
设点P横坐标为m.
(1)求直线AB所对应的函数表达式.
(2)用含m的代数式表示线段PQ的长.
(3)以PQ、QM为邻边作矩形PQMN,求矩形PQMN的周长为9时m的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com