练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知实数 a、b、c满足 a+b2＝1，a+1＝c2﹣2c，若 m＝2a2+5b2，实数 m的取值范围是______

    【答案】2≤m≤23

    【解析】

    根据a+b2＝1，a+1＝c2﹣2c，可以求得a的取值范围，再根据m＝2a2+5b2和二次函数的性质即可求得m的取值范围．

    ∵a+b2＝1，a+1＝c2﹣2c，∴b2＝1﹣a，a+2＝（c﹣1）2，∴，得：﹣2≤a≤1．

    ∵b2＝1﹣a，∴m＝2a2+5b2＝2a2+5（1﹣a）＝2a2﹣5a+5．

    ∵m＝2a2﹣5a+5的对称轴是直线a，a＞0，∴当a时，m随a的增大而减小．

    ∵﹣2≤a≤1，∴当a＝﹣2时，m取得最大值，此时m＝23，当a＝1时，m取得最小值，此时m＝2，∴m的取值范围是2≤m≤23．

    故答案为：2≤m≤23．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

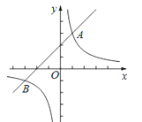
    【题目】如图，一次函数y=x+2的图象与反比例函数y=（k≠0）的图象交于A，B两点，且点A的坐标为（1，m）．

    （1）求反比例函数y=（k≠0）的表达式；

    （2）若P是y轴上一点，且满足△ABP的面积为6，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数y=为反比例函数．

    （1）求k的值；

    （2）它的图象在第　 　象限内，在各象限内，y随x增大而　 　；（填变化情况）

    （3）求出﹣2≤x≤﹣时，y的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

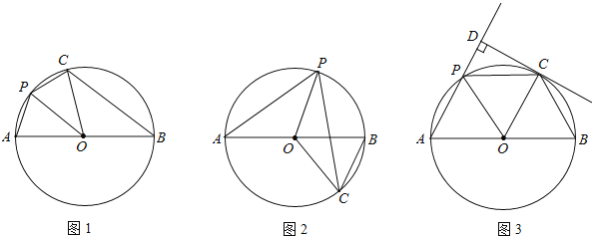
    【题目】已知，AB是⊙O的直径，点P在弧AB上（不含点A、B），把△AOP沿OP对折，点A的对应点C恰好落在⊙O上．

    （1）当P、C都在AB上方时（如图1），判断PO与BC的位置关系（只回答结果）；

    （2）当P在AB上方而C在AB下方时（如图2），（1）中结论还成立吗？证明你的结论；

    （3）当P、C都在AB上方时（如图3），过C点作CD⊥直线AP于D，且CD是⊙O的切线，证明：AB=4PD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

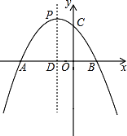
    【题目】如图，已知抛物线y=﹣x2﹣2x+m+1与x轴交于A（x1 ， 0）、B（x2 ， 0）两点，且x1＜0，x2＞0，与y轴交于点C，顶点为P．（提示：若x1 ， x2是一元二次方程ax2+bx+c=0（a≠0）的两个实根，则x1+x2=﹣ ，x1x2= ）

    (1)求m的取值范围；

    (2)若OA=3OB，求抛物线的解析式；

    (3)在(2)中抛物线的对称轴PD上，存在点Q使得△BQC的周长最短，试求出点Q的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

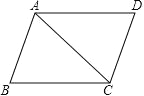
    【题目】如图，四边形ABCD 是平行四边形，AB＝c，AC＝b，BC＝a，抛物线 y＝ax2+bx﹣c 与 x 轴的一个交点为（m，0）．

    （1）若四边形ABCD是正方形，求抛物线y＝ax2+bx﹣c的对称轴；

    （2）若 m＝c，ac﹣4b＜0，且 a，b，c为整数，求四边形 ABCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AD是△ABC的角平分线，⊙O经过A、B、D三点，过点B作BE∥AD，交⊙O于点E，连接ED．

    （1）求证：ED∥AC；

    （2）连接AE，试证明：ABCD=AEAC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某数学兴趣小组的同学利用标杆测量旗杆（AB）的高度：将一根5米高的标杆（CD）竖在某一位置，有一名同学站在一处与标杆、旗杆成一条直线，此时他看到标杆顶端与旗杆顶端重合，另外一名同学测得站立的同学离标杆3米，离旗杆30米．如果站立的同学的眼睛距地面（EF）1.6米，求旗杆的高度AB．

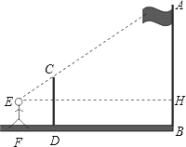
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】瑞安市文化创意实践学校是一所负责全市中小学生素质教育综合实践活动的公益类事业单位，学校目前可开出：创意手工创意表演、科技制作（创客）、文化传承、户外拓展等5个类别20多个项目课程．

    （1）学校3月份接待学生1000人，5月份增长到2560人，求该学校接待学生人数的平均月增长率是多少？

    （2）在参加“创意手工”体验课程后，小明发动本校同学将制作的作品义卖募捐．当作品卖出的单价是2元时，每天义卖的数量是150件；当作品的单价每涨高1元时，每天义卖的数量将减少10件．问：在作品单价尽可能便宜的前提下，当单价定为多少元时，义卖所得的金额为600元？

    查看答案和解析>>

    同步练习册答案