
����Ŀ��ʵ��̽����
��A��B���������IJ�����A��������������ȫ��ͬ��С�ֱ��������1��2��B��������������ȫ��ͬ��С�ֱ�������֣�1����2�ͣ�3��С����A���������ȡ��һ��С��¼����е�����Ϊx���ٴ�B���������ȡ��һ��С��¼����е�����Ϊy��������ȷ����![]() ��һ������Ϊ
��һ������Ϊ![]() ��
��
��1�����б�����״ͼ�ķ���д����Q�����п������ꣻ
��2�����Q����ֱ��![]() �ϵĸ��ʣ�
�ϵĸ��ʣ�
���𰸡���1����Q�������У�1��-1������1��-2������1��-3������2��-1������2��-2����2��-3������2��![]() .
.
��������
�����������1�����б���������ͼ���оٳ�����ʵ���ȡ�Ľ��������д����Q�����п������ꣻ��2������Щ�����������һ�κ�������ʽ���������������ʽ�ĵ�ĸ����������е�ĸ�����Ϊ���ڸ�ֱ���ϵĸ���.
�����������1��С����A���������ȡ��һ��С��x�������ֵȿ��ܽ�����ֱ���1,2.�ٴ�B���������ȡ��һ��С��y�������ֵȿ��ܽ�����ֱ���-1��-2��-3�����Թ���6�ֵȿ��ܽ������Q������ֱ��ǣ�1��-1������1��-2������1��-3������2��-1������2��-2����2��-3������2������Щ�������ֱ����ֱ��y=x-3,�����������ʽ���е㣨1��-2����2��-1�������ֵȿ��ܽ�������Ե�Q����ֱ��y=x-3�ϵĸ�����P=![]() =
=![]() ��
��


 ����ѧ���ʱѧ����ϵ�д�
����ѧ���ʱѧ����ϵ�д� �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����ѧ��������������ѧУ�ƻ�������������ѡ�Σ�A���鷨��B���滭��C��������D���赸��Ϊ�˽�ѧ�������Ź��ε�ϲ���������ȫУ��Χ�������ȡ������ѧ�������ʾ����飨ÿ���������ѧ������ѡ�����ֻ��ѡ������һ�ţ��������ݽ��������������Ƴ�����������������ͳ��ͼ������ͼ��������Ϣ����������⣺
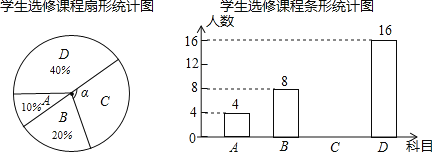
��1�����ε����ѧ�����ж����ˣ�����ͳ��ͼ�С����Ķ����Ƕ��٣�
��2���������ͳ��ͼ����������
��3��ѧУΪ�ٰ�2018���У�Ļ������ڣ�������A���鷨��B���滭��C��������D���赸����������ʽ��ѡ�������������һ���µĽ�Ŀ��ʽ�������б�������״ͼ���ѡ���鷨�����������һ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����¥¥��![]() �ף���¥�����ڼ�¥�������棬��֪���ض�������
�ף���¥�����ڼ�¥�������棬��֪���ض�������![]() ʱ̫��������ˮƽ��ļн�Ϊ
ʱ̫��������ˮƽ��ļн�Ϊ![]() ����ʱ��
����ʱ��
�������¥���![]() �ף���ô��¥��Ӱ��������¥���ж�ߣ�________
�ף���ô��¥��Ӱ��������¥���ж�ߣ�________
�������¥��Ӱ�Ӹպò�������¥�ϣ���ô��¥�ľ���Ӧ����________�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
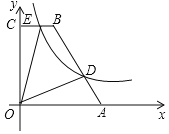
����Ŀ����ͼ�����ı���OABC�У�![]() ����
����![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() ����DΪAB��һ�㣬��
����DΪAB��һ�㣬��![]() ��˫����
��˫����![]() ������D����BC�ڵ�E
������D����BC�ڵ�E
![]() ��˫���ߵĽ���ʽ��
��˫���ߵĽ���ʽ��
![]() ���ı���ODBE�������
���ı���ODBE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2+2x����m��2����0��ʵ������
��1����m��ȡֵ��Χ��
��2����������һ����Ϊx��1����m��ֵ����һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
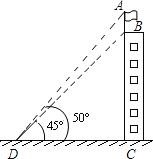
����Ŀ�������������ճ������г��������⣬��ͼ��������BC���ݶ���һ�����AB���ӵ�����D�㴦�۲���˶���A������Ϊ50�㣬�۲���˵ײ�B�������Ϊ45�㣬�����õIJο����ݣ�sin50���0.8��tan50���1.2��
��1������֪CD=20�ף�������BC�ĸ߶ȣ�
��2������֪��˵ĸ߶�AB=5�ף�������BC�ĸ߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
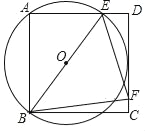
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2����E�ڱ�AD��(����A��D�غ�)����F�ڱ�CD�ϣ�����EBF=45��������ABE�����Բ��O��CD�����У�
(1)����O�İ뾶����
(2)����BEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�Ƶ�D��ת����C����BC�ϵĵ�H������Bǡ�����ڵ�A������ƽ���ı���DHAE����BH=2��CH=3����DC=_____��
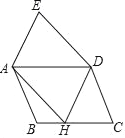
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB�������ߵĽ�����A(0��-3)��B(5��9)����֪�����ߵĶ���D�ĺ�������2.

(1)�������ߵĽ���ʽ���������ꣻ
(2)��![]() �����Ƿ����һ��C����A��B��ɵ��������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
�����Ƿ����һ��C����A��B��ɵ��������Σ������ڣ������C�����꣬�������ڣ���˵�����ɣ�
(3)��ֱ��AB���·�����������һ��P������PA��PBʹ�á�PAB�����������������ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com