
【题目】如图,甲楼楼高![]() 米,乙楼座落在甲楼的正北面,已知当地冬至中午
米,乙楼座落在甲楼的正北面,已知当地冬至中午![]() 时太阳光线与水平面的夹角为
时太阳光线与水平面的夹角为![]() ,此时求:
,此时求:
①如果两楼相距![]() 米,那么甲楼的影子落在乙楼上有多高?________
米,那么甲楼的影子落在乙楼上有多高?________
②如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应当是________米.

【答案】(16![]() )米 16
)米 16![]() .
.
【解析】
①设CE⊥AB于点E,那么在Rt△AEC中,∠AEC=90°,∠ACE=30°,解直角三角形AEC可以求得AE的长,求得BE=AB-AE即可解题;
②要使甲楼的影子刚好不落在乙楼上,则使得两楼距离=![]() AB即可.
AB即可.
①设冬天太阳最低时,甲楼最高处A点的影子落在乙楼的C处,那么图中CD的长度就是甲楼的影子在乙楼上的高度,设CE⊥AB于点E,
那么在Rt△AEC中,∠AEC=90°,∠ACE=30°,EC=20米
∵![]() =tan∠ACE,
=tan∠ACE,
∴AE=ECtan∠ACE=20tan30°=20×![]() =
=![]() (米),
(米),
CD=EB=ABAE=16![]() (米);
(米);
②设点A的影子落到地面上某一点F,则在Rt△ABF中,∠AFB=30°,AB=16米,
所以BF=ABcot∠AFB=16![]() (米).
(米).
所以要使甲楼的影子不影响乙楼,那么乙楼距离甲楼至少要16![]() 米.
米.
故答案为①(16![]() )米;②16
)米;②16![]() .
.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
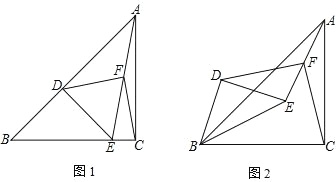
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
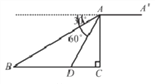
【题目】如图,某无人机于空中A处探测到目标B、D的俯角分别是30°、60°,此时无人机的飞行高度AC为60m.随后无人机从A处继续水平飞行30![]() m到达A′处.
m到达A′处.
(1)求A、B之间的距离:
(2)求从无人机A′上看目标D的俯角的正切值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,以点
的中点,以点![]() 为圆心、
为圆心、![]() 长为半径作圆,恰好点
长为半径作圆,恰好点![]() 在
在![]() 上,连接
上,连接![]() ,若
,若![]() ,下列说法中不正确的是( )
,下列说法中不正确的是( )
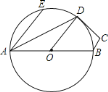
A. D是劣弧BE的中点 B. CD是⊙O的切线 C. AE//OD D. ∠DOB=∠EAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,测量队为了测量某地区山顶![]() 的海拔高度,选
的海拔高度,选![]() 点作为观测点,从
点作为观测点,从![]() 点测量山顶
点测量山顶![]() 的仰角(视线在水平线上方,与水平线所夹的角)为
的仰角(视线在水平线上方,与水平线所夹的角)为![]() ,在比例尺为
,在比例尺为![]() 的该地区等高线地形图上,量得这两点的图上距离为
的该地区等高线地形图上,量得这两点的图上距离为![]() 厘米,则山顶
厘米,则山顶![]() 的海拔高度为( )
的海拔高度为( )
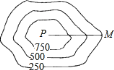
A. ![]() 米 B.
米 B. ![]() 米 C.
米 C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
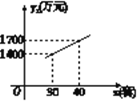
【题目】已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套.已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图9所示的函数关系.
(1)直接写出y2与x之间的函数关系式,并求月产量x的取值范围;
(2)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
有A,B两个不透明的布袋,A布袋中有两个完全相同的小球,分别标有数字1和2.B布袋中有三个完全相同的小球,分别标有数字-1,-2和-3.小明从A布袋中随机取出一个小球,记录其标有的数字为x,再从B布袋中随机取出一个小球,记录其标有的数字为y,这样就确定点![]() 的一个坐标为
的一个坐标为![]() .
.
(1)用列表或画树状图的方法写出点Q的所有可能坐标;
(2)求点Q落在直线![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
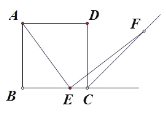
【题目】如图,四边形 ABCD 是正方形,点 E是 BC边上任意一点, AEF 90°,且EF 交正方形外角的平分线 CF 于点 F.求证:AE=EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com