
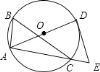
【题目】如图,![]() 内接于
内接于![]() ,
,![]() ,
,![]() 是直径,过点
是直径,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于
的延长线于![]() ,如果
,如果![]() ,
,![]() ,则
,则![]() ________.
________.
【答案】![]()
【解析】
连DC,过A点作AF⊥BC,由∠B=60°,得∠ADC=60°,再由AD为直径,DE为⊙O的切线,可得∠ADE=90°,∠DCE=90°,∠DAE=30°,
由CE=![]() ,利用含30度的直角三角形的三边的关系即可求得DC=
,利用含30度的直角三角形的三边的关系即可求得DC=![]() EC=
EC=![]() ×
×![]() =
=![]() ,AD=2
,AD=2![]() ,AC=
,AC=![]() ×
×![]() =
=![]() ,而AB=2,由此可得到△OAB为等腰直角三角形,则∠AOB=90°,∠ACB=45°;在Rt△ACF中,AC=
,而AB=2,由此可得到△OAB为等腰直角三角形,则∠AOB=90°,∠ACB=45°;在Rt△ACF中,AC=![]() CF,所以CF=
CF,所以CF=![]() ×
×![]() =
=![]() ,在Rt△ABF中,AB=2BF,所以BF=
,在Rt△ABF中,AB=2BF,所以BF=![]() ×2=1,于是得到BC的长.
×2=1,于是得到BC的长.
连DC,OB,过A点作AF⊥BC,如图,
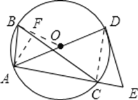
∵∠B=60°,
∴∠ADC=60°,
又∵DE为⊙O的切线,
∴∠ADE=90°,
而AD为直径,
∴∠DCE=90°,则∠DAE=30°,
∵CE=![]() ,
,
∴DC=![]() EC=
EC=![]() ×
×![]() =
=![]() ,
,
∴在Rt△ADC中,AD=2![]() ,AC=
,AC=![]() ×
×![]() =
=![]() ,
,
在△OAB中,OB=OA=![]() ,AB=2,所以△OAB为等腰直角三角形,
,AB=2,所以△OAB为等腰直角三角形,
∴∠AOB=90°,
∴∠ACB=45°,
在Rt△ACF中,AC=![]() CF,所以CF=
CF,所以CF=![]() ×
×![]() =
=![]() ,
,
在Rt△ABF中,AB=2BF,所以BF=![]() ×2=1,
×2=1,
所以BC=BF+FC=![]() +1.
+1.
故答案为1+![]() .
.


科目:初中数学 来源: 题型:
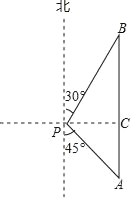
【题目】随着航母编队的成立,我国海军日益强大,2018年4月12日,中央军委在南海海域降重举行海上阅兵,在阅兵之前我军加强了海上巡逻,如图,我军巡逻舰在某海域航行到A处时,该舰在观测点P的南偏东45°的方向上,且与观测点P的距离PA为400海里;巡逻舰继续沿正北方向航行一段时间后,到达位于观测点P的北偏东30°方向上的B处,问此时巡逻舰与观测点P的距离PB为多少海里?(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,结果精确到1海里).
≈1.732,结果精确到1海里).
查看答案和解析>>
科目:初中数学 来源: 题型:
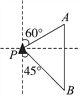
【题目】如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时B处与灯塔P的距离约为_______nmile.(结果取整数,参考数据:![]() =1.7,
=1.7, ![]() ≈ 1.4)
≈ 1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
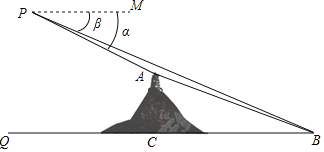
【题目】数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离.如图,无人机所在位置P与岚光阁阁顶A、湖心亭B在同一铅垂面内,P与B的垂直距离为300米,A与B的垂直距离为150米,在P处测得A、B两点的俯角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)
﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲楼楼高![]() 米,乙楼座落在甲楼的正北面,已知当地冬至中午
米,乙楼座落在甲楼的正北面,已知当地冬至中午![]() 时太阳光线与水平面的夹角为
时太阳光线与水平面的夹角为![]() ,此时求:
,此时求:
①如果两楼相距![]() 米,那么甲楼的影子落在乙楼上有多高?________
米,那么甲楼的影子落在乙楼上有多高?________
②如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应当是________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一架
,一架![]() 米长的梯子
米长的梯子![]() 斜靠在与地面
斜靠在与地面![]() 垂直的墙
垂直的墙![]() 上,梯子
上,梯子![]() 与地面
与地面![]() 的倾斜角
的倾斜角![]() 为
为![]() .
.
![]() 求
求![]() 与
与![]() 的长;
的长;
![]() 若梯子顶端
若梯子顶端![]() 沿
沿![]() 下滑,如图
下滑,如图![]() ,设
,设![]() 点下滑至
点下滑至![]() 点,
点,![]() 点向右滑行至
点向右滑行至![]() 点.若
点.若![]() ,试求梯子顶端
,试求梯子顶端![]() 沿
沿![]() 下滑多少米;
下滑多少米;
![]() 若梯子顶端
若梯子顶端![]() 沿
沿![]() 下滑,如图
下滑,如图![]() ,设
,设![]() 点下滑至
点下滑至![]() 点,
点,![]() 点向右滑行至
点向右滑行至![]() 点,梯子
点,梯子![]() 的中点
的中点![]() ,也随之运动到点
,也随之运动到点![]() ,若
,若![]() ,试求
,试求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
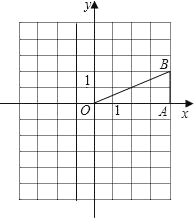
【题目】如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A.
(1)画出将△OAB绕原点顺时针旋转90°后所得的△OA1B1,并写出点A1、B1的坐标;
(2)画出△OAB关于原点O的中心对称图形△OA2B2,并写出点A2、B2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com