
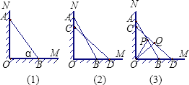
【题目】如图![]() ,一架
,一架![]() 米长的梯子
米长的梯子![]() 斜靠在与地面
斜靠在与地面![]() 垂直的墙
垂直的墙![]() 上,梯子
上,梯子![]() 与地面
与地面![]() 的倾斜角
的倾斜角![]() 为
为![]() .
.
![]() 求
求![]() 与
与![]() 的长;
的长;
![]() 若梯子顶端
若梯子顶端![]() 沿
沿![]() 下滑,如图
下滑,如图![]() ,设
,设![]() 点下滑至
点下滑至![]() 点,
点,![]() 点向右滑行至
点向右滑行至![]() 点.若
点.若![]() ,试求梯子顶端
,试求梯子顶端![]() 沿
沿![]() 下滑多少米;
下滑多少米;
![]() 若梯子顶端
若梯子顶端![]() 沿
沿![]() 下滑,如图
下滑,如图![]() ,设
,设![]() 点下滑至
点下滑至![]() 点,
点,![]() 点向右滑行至
点向右滑行至![]() 点,梯子
点,梯子![]() 的中点
的中点![]() ,也随之运动到点
,也随之运动到点![]() ,若
,若![]() ,试求
,试求![]() 的长.
的长.

【答案】(1)![]() 米
米![]() 米;(2)梯子的顶端沿
米;(2)梯子的顶端沿![]() 下滑
下滑![]() 米;(3)
米;(3)![]() (米).
(米).
【解析】
(1)在直角△AOB中,已知斜边AB,和锐角∠ABO,即可根据正弦和余弦的定义求得OA,OB的长;
(2)利用AC:BD=2:3,设AC=2x(米)BD=3x(米)CD=4米,利用勾股定理列出关系式即可求得下滑的长度;
(3)根据P、Q分别是Rt△AOB和Rt△COD斜边上的中线求得PO=PA、QO=QC,从而得到∠PAO=∠AOP,∠QCO=∠COQ,然后求得QCO=45°,利用解直角三角形求得AC的长即可.
解:(1)![]() 中,
中,![]()
![]() 米,
米,![]() 米,
米,![]() 米
米
![]() (米),
(米),![]() (米),
(米),![]() 米
米
![]() 中,
中,![]()
![]() ,
,
解得![]() (舍去)
(舍去)![]() (米)
(米)
梯子的顶端沿![]() 下滑
下滑![]() 米.
米.
![]() 分别是
分别是![]() 斜边上的中点
斜边上的中点
∴![]()
∴![]() …
…
∴![]()
∵![]()
∴![]() …
…
![]() ,
,
![]() (米).
(米).


科目:初中数学 来源: 题型:
【题目】某商店将每件进价为![]() 元的某种商品每件
元的某种商品每件![]() 元出售,一天可销出约
元出售,一天可销出约![]() 件.该店想通过降低售价,增加销售量的办法来提高利润.经过市场调查,发现这种商品单价每降低
件.该店想通过降低售价,增加销售量的办法来提高利润.经过市场调查,发现这种商品单价每降低![]() 元,其销售量可增加
元,其销售量可增加![]() 件,将这种商品的售价降低
件,将这种商品的售价降低![]() 元时,则销售利润
元时,则销售利润![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
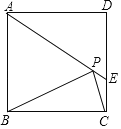
【题目】如图,在正方形ABCD中,AD=2![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
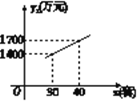
【题目】已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套.已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图9所示的函数关系.
(1)直接写出y2与x之间的函数关系式,并求月产量x的取值范围;
(2)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
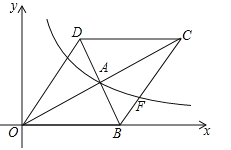
【题目】如图,在平面直角坐标系中,菱形OBCD的边OB在x轴上,反比例函数![]() (x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(x>0)的图象经过菱形对角线的交点A,且与边BC交于点F,点A的坐标为(4,2).
(1)求反比例函数的表达式;
(2)求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地发生8.1级强烈地震,我国积极组织抢险队赴地震灾区参与抢险工作.如图,某探测队在地面A,B两处均探测出建筑物下方C处有生命迹象,已知探测线与地面的夹角分别是25°和60°,且AB=4米,求该生命迹象所在位置C的深度.(结果精确到1米.参考数据:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
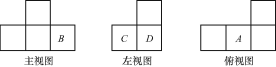
【题目】由若干小立方体叠成的几何体的三视图如图所示:
(1)分别说出A,B,C,D这4个方格位置上的小立方体的个数;
(2)这个几何体共有多少个小立方体?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com