
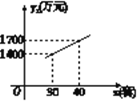
【题目】已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套.已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图9所示的函数关系.
(1)直接写出y2与x之间的函数关系式,并求月产量x的取值范围;
(2)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
【答案】(1)y2=30x+500,25≤x≤40;(2)当月产量为35套时,利润最大,最大利润是1 950万元.
【解析】
(1)设函数关系式为y2=kx+b,把(30,1400)(40,1700)代入求解即可;根据题中条件“每套产品的生产成本不高于50万元,每套产品的售价不低于90万元”列出不等式组求解月产量x的范围;
(2)根据等量关系“设备的利润=每台的售价×月产量-生产总成本”列出函数关系式求得最大值.
(1)设函数关系式为y2=kx+b,把坐标(30,1400)(40,1700)代入,
得![]() ,解得:
,解得:![]() ,
,
∴函数关系式y2=30x+500,
依题意得:![]() ,
,
解得:25≤x≤40;
(2)∵W=xy1-y2=x(170-2x)-(500+30x)=-2x2+140x-500,
∴W=-2(x-35)2+1950,
∵25≤x≤40,
∴当x=35时,W最大=1950.
答:当月产量为35件时,利润最大,最大利润是1950万元.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
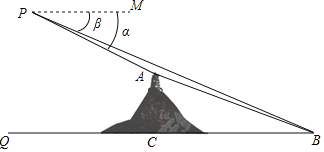
【题目】数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离.如图,无人机所在位置P与岚光阁阁顶A、湖心亭B在同一铅垂面内,P与B的垂直距离为300米,A与B的垂直距离为150米,在P处测得A、B两点的俯角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)
﹣1,试求岚光阁与湖心亭之间的距离AB.(计算结果若含有根号,请保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲楼楼高![]() 米,乙楼座落在甲楼的正北面,已知当地冬至中午
米,乙楼座落在甲楼的正北面,已知当地冬至中午![]() 时太阳光线与水平面的夹角为
时太阳光线与水平面的夹角为![]() ,此时求:
,此时求:
①如果两楼相距![]() 米,那么甲楼的影子落在乙楼上有多高?________
米,那么甲楼的影子落在乙楼上有多高?________
②如果甲楼的影子刚好不落在乙楼上,那么两楼的距离应当是________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,一架
,一架![]() 米长的梯子
米长的梯子![]() 斜靠在与地面
斜靠在与地面![]() 垂直的墙
垂直的墙![]() 上,梯子
上,梯子![]() 与地面
与地面![]() 的倾斜角
的倾斜角![]() 为
为![]() .
.
![]() 求
求![]() 与
与![]() 的长;
的长;
![]() 若梯子顶端
若梯子顶端![]() 沿
沿![]() 下滑,如图
下滑,如图![]() ,设
,设![]() 点下滑至
点下滑至![]() 点,
点,![]() 点向右滑行至
点向右滑行至![]() 点.若
点.若![]() ,试求梯子顶端
,试求梯子顶端![]() 沿
沿![]() 下滑多少米;
下滑多少米;
![]() 若梯子顶端
若梯子顶端![]() 沿
沿![]() 下滑,如图
下滑,如图![]() ,设
,设![]() 点下滑至
点下滑至![]() 点,
点,![]() 点向右滑行至
点向右滑行至![]() 点,梯子
点,梯子![]() 的中点
的中点![]() ,也随之运动到点
,也随之运动到点![]() ,若
,若![]() ,试求
,试求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
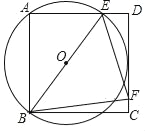
【题目】如图,正方形ABCD的边长为2,点E在边AD上(不与A,D重合),点F在边CD上,且∠EBF=45°,若△ABE的外接圆⊙O与CD边相切.
(1)求⊙O的半径长;
(2)求△BEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD内接于⊙O,点E在CB的延长线上,连结AC、AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=![]() ,tan∠ADC=3,求BE的长.
,tan∠ADC=3,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com