
【题目】如图,![]() ,
,![]() 是双曲线
是双曲线![]() 与直线
与直线![]() 的两个交点,
的两个交点,![]() 、
、![]() 都垂直于
都垂直于![]() 轴,垂足为
轴,垂足为![]() 、
、![]() ,那么四边形
,那么四边形![]() 的面积是( )
的面积是( )
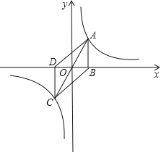
A. 3 B. 6 C. 9 D. 12
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
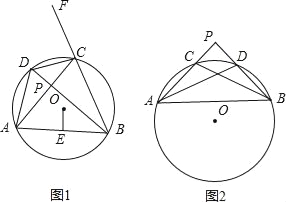
【题目】已知:如图1,四边形ABCD内接于⊙O,AC⊥BD于点P,OE⊥AB于点E,F为BC延长线上一点.
(1)求证:∠DCF=∠DAB;
(2)求证:![]() ;
;
(3)当图1中点P运动到圆外时,即AC、BD的延长线交于点P,且∠P=90°时(如图2所示),(2)中的结论是否成立?如果成立请给出你的证明,如果不成立请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(2,0),其对称轴是直线x=﹣1,直线y=3恰好经过顶点.有下列判断:①当x<﹣2时,y随x增大而减小; ②ac<0; ③a﹣b+c<0; ④方程ax2+bx+c=0的两个根是x1=2,x2=﹣4;⑤当m≤3时,方程ax2+bx+c=m有实数根.其中正确的是( )
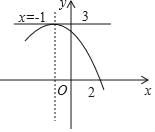
A. ①②③ B. ①②④ C. ②④⑤ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
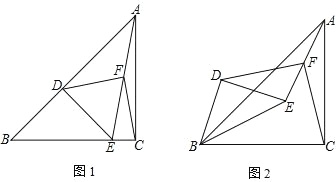
【题目】已知如图 1,在△ABC 中,∠ACB=90°,BC=AC,点 D 在 AB 上,DE⊥AB交 BC 于 E,点 F 是 AE 的中点
(1) 写出线段 FD 与线段 FC 的关系并证明;
(2) 如图 2,将△BDE 绕点 B 逆时针旋转α(0°<α<90°),其它条件不变,线段 FD 与线段 FC 的关系是否变化,写出你的结论并证明;
(3) 将△BDE 绕点 B 逆时针旋转一周,如果 BC=4,BE=2![]() ,直接写出线段 BF 的范围.
,直接写出线段 BF 的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将每件进价为![]() 元的某种商品每件
元的某种商品每件![]() 元出售,一天可销出约
元出售,一天可销出约![]() 件.该店想通过降低售价,增加销售量的办法来提高利润.经过市场调查,发现这种商品单价每降低
件.该店想通过降低售价,增加销售量的办法来提高利润.经过市场调查,发现这种商品单价每降低![]() 元,其销售量可增加
元,其销售量可增加![]() 件,将这种商品的售价降低
件,将这种商品的售价降低![]() 元时,则销售利润
元时,则销售利润![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 购买江苏省体育彩票有“中奖”与“不中奖”两种情况,所以中奖的概率是![]()
B. 国家级射击运动员射靶一次,正中靶心是必然事件
C. 如果在若干次试验中一个事件发生的频率是![]() ,那么这个事件发生的概率一定也是
,那么这个事件发生的概率一定也是![]()
D. 如果车间生产的零件不合格的概率为![]() ,那么平均每检查1000个零件会查到1个次品
,那么平均每检查1000个零件会查到1个次品
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(3,﹣6)是二次函数y=ax2上的一点,则这二次函数的解析式是 .
【答案】y=﹣![]() x2
x2
【解析】
试题分析:将点A(3,﹣6)代入y=ax2,利用待定系数法法求该二次函数的解析式即可得﹣6=9a,
解得a=﹣![]() ;因此该二次函数的解析式为:y=﹣
;因此该二次函数的解析式为:y=﹣![]() x2.
x2.
考点:待定系数法求二次函数解析式
【题型】填空题
【结束】
15
【题目】在一个不透明的口袋中装有8个红球和若干个白球,它们除颜色外其它完全相同,通过多次摸球试验后发现,摸到红球的频率稳定在40%附近,则口袋中白球可能有________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某无人机于空中A处探测到目标B、D的俯角分别是30°、60°,此时无人机的飞行高度AC为60m.随后无人机从A处继续水平飞行30![]() m到达A′处.
m到达A′处.
(1)求A、B之间的距离:
(2)求从无人机A′上看目标D的俯角的正切值
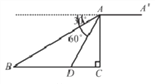
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种高新技术设备的生产成本不高于50万元/套,售价不低于90万元/套.已知这种设备的月产量x(套)与每套的售价y1(万元)之间满足关系式y1=170-2x,月产量x(套)与生产总成本y2(万元)存在如图9所示的函数关系.
(1)直接写出y2与x之间的函数关系式,并求月产量x的取值范围;
(2)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
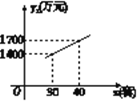
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com