
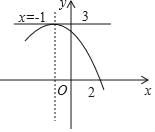
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ���㣨2��0������Գ�����ֱ��x=��1��ֱ��y=3ǡ�þ������㣮�������жϣ��ٵ�x����2ʱ��y��x�������С�� ��ac��0�� ��a��b+c��0�� �ܷ���ax2+bx+c=0����������x1=2��x2=��4���ݵ�m��3ʱ������ax2+bx+c=m��ʵ������������ȷ���ǣ�������
A. �٢ڢ� B. �٢ڢ� C. �ڢܢ� D. �ڢۢ�
���𰸡�C
��������
�������ߵĿ��ڷ����ж�a��0�Ĺ�ϵ������������y��Ľ����ж�c��0�Ĺ�ϵ��Ȼ����ݶԳ��ἰ��������x�ύ������������������������ý��۽����жϣ�
����ͼ��֪����x��-2ʱ��y��x��������ʴ���
�������߿��ڷ������£���a��0��
��������y�ύ�������ᣬ��c��0��
����ac��0������ȷ��
��������֪����x=-1ʱ��y=3��0��
����a-b+c��0���ʴ���
��������֪����������x�����һ������㣨2��0������ֱ��x=-1�Գƣ������������x�����һ���������ǣ�-4��0�������Է���ax2+bx+c=0����������x1=2��x2=-4������ȷ��
��������֪����m��3ʱ��ֱ��y=m��������y=ax2+bx+c��a��0���н��㣬���ԣ�����ax2+bx+c=m��ʵ����������ȷ��
������������ȷ�Ľ����ǣ��ڢܢ���
��ѡ��C��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
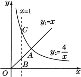
����Ŀ������y1=x(x��0),y2=![]() (x>0)��ͼ����ͼ��ʾ,���н���:
(x>0)��ͼ����ͼ��ʾ,���н���:
��������ͼ��Ľ�������ΪA(2,2);
�ڵ�x>2ʱ,y2>y1;
��ֱ��x=1�ֱ�����������ͼ���ཻ��B,C����,���߶�BC�ij�Ϊ3;
�ܵ�x������ʱ,y1��ֵ��x�����������,y2��ֵ��x�����������,������ȷ����(����)
A. �٢� B. �٢� C. �ڢ� D. �٢ۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��ƽ��ֱ�������е�һ�㣬��
��ƽ��ֱ�������е�һ�㣬��![]() ��
��![]() �Ḻ������һ���㣬����
�Ḻ������һ���㣬����![]() ������
������![]() ����
Ϊ����![]() ���Ϸ�������
���Ϸ�������![]() ��������
��������![]() �����
�����![]() �������
�ĺ�������![]() ������ú�
������ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ������꣬��ô
������꣬��ô![]() ���������_____��
���������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B=90�㣬AB=12��BC=24������P�ӵ�A��ʼ�ر�AB���յ�B��ÿ��2����λ���ȵ��ٶ��ƶ�������Q�ӵ�B��ʼ�ر�BC��ÿ��4����λ���ȵ��ٶ����յ�C�ƶ��������P��Q�ֱ�ӵ�A��Bͬʱ��������ô��PBQ�����S�����ʱ��t��s����α仯��д��������ϵʽ��t��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н��ۣ���ab��0����a+3b+9c��0����4a+b=0���ܵ�y=��2ʱ��x��ֵֻ��Ϊ0����3b��c��0��������ȷ�ĸ����ǣ�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
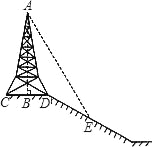
����Ŀ����ͼ����б�µĶ�����һ����AB��B��CD���е㣬CD��ˮƽ�ģ�������������£���ӰDE���������ϣ���֪����������CD=12 m����Ӱ��DE=18 m��С����С�������߶���1.6m��ͬһʱ�̣�С��վ�ڵ�E����Ӱ���������ϣ�С��վ��ƽ���ϣ�Ӱ��Ҳ��ƽ���ϣ����˵�Ӱ���ֱ�Ϊ2m��1m����ô����ABΪ��������
A. 24m B. 22m C. 20m D. 18m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
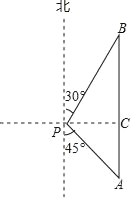
����Ŀ�����ź�ĸ��ӵij������ҹ���������ǿ��2018��4��12�գ������ί���Ϻ������ؾ��к����ı������ı�֮ǰ�Ҿ���ǿ�˺���Ѳ�ߣ���ͼ���Ҿ�Ѳ�߽���ij�����е�A��ʱ���ý��ڹ۲��P����ƫ��45���ķ����ϣ�����۲��P�ľ���PAΪ400���Ѳ�߽�����������������һ��ʱ�����λ�ڹ۲��P�ı�ƫ��30�������ϵ�B�����ʴ�ʱѲ�߽���۲��P�ľ���PBΪ���ٺ�����ο����ݣ�![]() ��1.414��
��1.414��![]() ��1.732�������ȷ��1�����
��1.732�������ȷ��1�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��˫����
��˫����![]() ��ֱ��
��ֱ��![]() ���������㣬
���������㣬![]() ��
��![]() ����ֱ��
����ֱ��![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ��
��![]() ����ô�ı���
����ô�ı���![]() ������ǣ� ��
������ǣ� ��
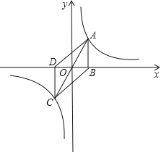
A. 3 B. 6 C. 9 D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
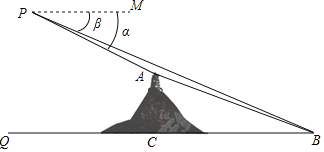
����Ŀ����ѧʵ���С��������в���ǵ����˻�������ɽ��������������֮ͤ��ľ��룮��ͼ�����˻�����λ��P�����A������ͤB��ͬһǦ�����ڣ�P��B�Ĵ�ֱ����Ϊ300�ף�A��B�Ĵ�ֱ����Ϊ150�ף���P�����A��B����ĸ��Ƿֱ�Ϊ����������tan��=![]() ��tan��=
��tan��=![]() ��1�������������֮ͤ��ľ���AB���������������и��ţ��뱣�����ţ�
��1�������������֮ͤ��ľ���AB���������������и��ţ��뱣�����ţ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com