
【题目】如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD. 
(1)求证:PQ是⊙O的切线;
(2)求证:BD2=ACBQ;
(3)若AC、BQ的长是关于x的方程x+ ![]() =m的两实根,且tan∠PCD=
=m的两实根,且tan∠PCD= ![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】
(1)证明:∵PQ∥AB,
∴∠ABD=∠BDQ=∠ACD,
∵∠ACD=∠BCD,
∴∠BDQ=∠ACD,
如图1,连接OB,OD,交AB于E,

则∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,
在△OBD中,∠OBD+∠ODB+∠O=180°,
∴2∠ODB+2∠O=180°,
∴∠ODB+∠O=90°,
∴PQ是⊙O的切线
(2)证明:如图2,连接AD,

由(1)知PQ是⊙O的切线,
∴∠BDQ=∠DCB=∠ACD=∠BCD=∠BAD,
∴AD=BD,
∵∠DBQ=∠ACD,
∴△BDQ∽△ACD,
∴ ![]() =
= ![]() ,
,
∴BD2=ACBQ
(3)解:方程x+ ![]() =m可化为x2﹣mx+4=0,
=m可化为x2﹣mx+4=0,
∵AC、BQ的长是关于x的方程x+ ![]() =m的两实根,
=m的两实根,
∴ACBQ=4,由(2)得BD2=ACBQ,
∴BD2=4,
∴BD=2,
由(1)知PQ是⊙O的切线,
∴OD⊥PQ,
∵PQ∥AB,
∴OD⊥AB,由(1)得∠PCD=∠ABD,
∵tan∠PCD= ![]() ,
,
∴tan∠ABD= ![]() ,
,
∴BE=3DE,
∴DE2+(3DE)2=BD2=4,
∴DE= ![]() ,
,
∴BE= ![]() ,
,
设OB=OD=R,
∴OE=R﹣ ![]() ,
,
∵OB2=OE2+BE2,
∴R2=(R﹣ ![]() )2+(
)2+( ![]() )2,
)2,
解得:R=2 ![]() ,
,
∴⊙O的半径为2 ![]()
【解析】(1)根据平行线的性质和圆周角定理得到∠ABD=∠BDQ=∠ACD,连接OB,OD,交AB于E,根据圆周角定理得到∠OBD=∠ODB,∠O=2∠DCB=2∠BDQ,根据三角形的内角和得到2∠ODB+2∠O=180°,于是得到∠ODB+∠O=90°,根据切线的判定定理即可得到结论;(2)证明:连接AD,根据等腰三角形的判定得到AD=BD,根据相似三角形的性质即可得到结论;(3)根据题意得到ACBQ=4,得到BD=2,由(1)知PQ是⊙O的切线,由切线的性质得到OD⊥PQ,根据平行线的性质得到OD⊥AB,根据三角函数的定义得到BE=3DE,根据勾股定理得到BE= ![]() ,设OB=OD=R,根据勾股定理即可得到结论.
,设OB=OD=R,根据勾股定理即可得到结论.
【考点精析】关于本题考查的分式方程的解和圆周角定理,需要了解分式方程无解(转化成整式方程来解,产生了增根;转化的整式方程无解);解的正负情况:先化为整式方程,求整式方程的解;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,AE⊥BC于E,∠ADC的平分线交AE于点O,以点O为圆心,OA为半径的圆经过点B,交BC于另一点F. 
(1)求证:CD与⊙O相切;
(2)若BF=24,OE=5,求tan∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了. 
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,点C在劣弧AB上(不与点A,B重合),点D为弦BC的中点,DE⊥BC,DE与AC的延长线交于点E,射线AO与射线EB交于点F,与⊙O交于点G,设∠GAB=ɑ,∠ACB=β,∠EAG+∠EBA=γ,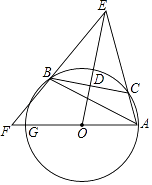
(1)点点同学通过画图和测量得到以下近似数据:
ɑ | 30° | 40° | 50° | 60° |
β | 120° | 130° | 140° | 150° |
γ | 150° | 140° | 130° | 120° |
猜想:β关于ɑ的函数表达式,γ关于ɑ的函数表达式,并给出证明:
(2)若γ=135°,CD=3,△ABE的面积为△ABC的面积的4倍,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
请根据上述信息解答下列问题:
(1)本次调查数据的众数落在组内,中位数落在组内;
(2)该辖区约有18000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( ) 
A.BO=OH
B.DF=CE
C.DH=CG
D.AB=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈ ![]() ,cos67°≈
,cos67°≈ ![]() ,tan67°≈
,tan67°≈ ![]() ,
, ![]() ≈1.73)
≈1.73)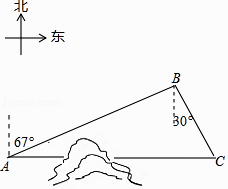
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,DE=CE,连接AE并延长交BC的延长线于点F.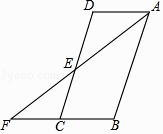
(1)求证:△ADE≌△FCE;
(2)若AB=2BC,∠F=36°.求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com