
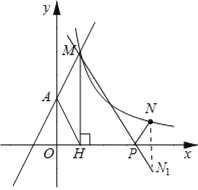
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.

【答案】(1)4 (2) ![]()
解:(1)由y=2x+2可知A(0,2),即OA=2.
∵tan∠AHO=2,∴OH=1.
∵MH⊥x轴,∴点M的横坐标为1.
∵点M在直线y=2x+2上,
∴点M的纵坐标为4.即M(1,4).
∵点M在![]() 上,
上,
∴k=1×4=4.
(2)存在.
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示).此时PM+PN最小.
∵点N(a,1)在反比例函数![]() 上,
上,
∴a=4.即点N的坐标为(4,1).
∵N与N1关于x轴的对称,N点坐标为(4,1),
∴N1的坐标为(4,﹣1).
设直线MN1的解析式为y=kx+b.
由![]() 解得
解得![]()
![]() .
.
∴直线MN1的解析式为![]() .
.
令y=0,得![]() .
.
∴P点坐标为![]() .
.
【解析】试题分析:(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】某数学兴趣小组同学进行测量大树CD高度的综合实践活动,如图,在点A处测得直立于地面的大树顶端C的仰角为36°,然后沿在同一剖面的斜坡AB行走13米至坡顶B处,然后再沿水平方向行走6米至大树脚底点D处,斜面AB的坡度(或坡比)i=1:2.4,那么大树CD的高度约为( )(参考数据:sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)
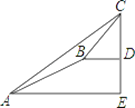
A. 8.1米 B. 17.2米 C. 19.7米 D. 25.5米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,转盘A的三个扇形面积相等,分别标有数字1,2,3,转盘B的四个扇形面积相等,分别有数字1,2,3,4.转动A、B转盘各一次,当转盘停止转动时,将指针所落扇形中的两个数字相乘(当指针落在四个扇形的交线上时,重新转动转盘).
(1)用树状图或列表法列出所有可能出现的结果;
(2)求两个数字的积为奇数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某同学周一至周五每天跳绳个数统计表:
星期 | 一 | 二 | 三 | 四 | 五 |
跳绳个数 | 160 | 160 | 180 | 200 | 170 |
则表示“跳绳个数”这组数据的中位数和众数分别是( )
A.180,160
B.170,160
C.170,180
D.160,200
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列定理中,不存在逆定理的是( )
A. 等边三角形的三个内角都等于60°
B. 在同一个三角形中,如果两边相等,那么它们所对的角也相等
C. 同位角相等,两直线平行
D. 全等三角形的对应角相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示.

(1)请你根据图中的数据填写表格:
姓名 | 平均数 | 众数 | 方差 |
甲 | 8 | ||
乙 | 8 | 2.8 |
(2)从平均数和方差相结合看,分析谁的成绩好些?从发展趋势来看,谁的成绩好些.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com