
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,M是AB边上的中点,点D、E分别是AC、BC边上的动点,连接DM 、ME、CM、DE, DE与CM相交于点F且∠DME=90°.则下列5个结论: (1)图中共有两对全等三角形;(2)△DEM是等腰三角形; (3)∠CDM=∠CFE;(4)AD2+BE2=DE2;(5)四边形CDME的面积发生改变.其中正确的结论有( )个.

A.2B.3C.4D.5
【答案】B
【解析】
根据等腰三角形的性质,三角形内角和定理,得出:△AMC≌△BMC、△AMD≌△CME、△CMD≌△BME,根据全等三角形的性质得出DM=ME得出△DEM是等腰三角形,及∠CDM=∠CFE,再逐个判断![]()
![]() 即可得出结论.
即可得出结论.
解:如图

在Rt△ABC中,∠ACB=90°,M为AB中点,AB=BC
∴AM=CM=BM,∠A=∠B=∠ACM=∠BCM=45°,∠AMC=∠BMC=90°
∵∠DME=90°.
∴∠1+∠2=∠2+∠3=∠3+∠4=90°
∴∠1=∠3,∠2=∠4
在△AMC和△BMC中

∴△AMC≌△BMC
在△AMD和△CME中

∴△AMD≌△CME
在△CDM和△BEM

∴△CMD≌△CME
共有3对全等三角形,故(1)错误
∵△AMD≌△BME
∴DM=ME
∴△DEM是等腰三角形,(2)正确
∵∠DME=90°.
∴∠EDM=∠DEM=45°,
∴∠CDM=∠1+∠A=∠1+45°,
∴∠EDM=∠3+∠DEM=∠3+45°,
∴∠CDM=∠CFE,故(3)正确
在Rt△CED中,![]()
∵CE=AD,BE=CD
∴![]() 故(4)正确
故(4)正确
(5)∵△ADM≌△CEM
∴![]()
∴![]() 不变,故(5)错误
不变,故(5)错误
故正确的有3个
故选:B


科目:初中数学 来源: 题型:
【题目】如图,花果山上有两只猴子在一棵树CD上的点B处,且BC=5m,它们都要到A处吃东西,其中一只猴子甲沿树爬下走到离树10m处的池塘A处,另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处.已知两只猴子所经过的路程相等,设BD为xm.
(1)请用含有x的整式表示线段AD的长为______m;
(2)求这棵树高有多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
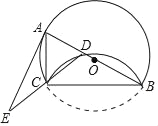
【题目】如图,以AB为直径作⊙O,点C为⊙O上一点,劣弧CB沿BC翻折,交AB于点D,过A作⊙O的切线交DC的延长线于点E.
(1)求证:AC=CD;
(2)已知tanE=![]() ,AC=2,求⊙O的半径.
,AC=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A按逆时针方向旋转至△AB′C′(B与B′,C与C′分别是对应顶点),使AB′⊥BC,B′C′分别交AC,BC于点D,E,已知AB=AC=5,BC=6,则DE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径作⊙O,点C为⊙O上一点,劣弧CB沿BC翻折,交AB于点D,过A作⊙O的切线交DC的延长线于点E.
(1)求证:AC=CD;
(2)已知tanE=![]() ,AC=2,求⊙O的半径.
,AC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某建筑商承接一条道路的铺设工程,需购置一批大小相同的花岗石板,它的长为160cm将这批花岗石板按如图①所示的两种方案进行切割(不计损耗,余料不再利用),切割后的M型和N型小花岗石板可拼成如图②所示的正方形(该图案不重叠无缝隙),图③的道路由若干个图②的正方形拼接而成(该图案不重叠无缝隙).

(1)M型小花岗石板的长AB= cm,宽AC= cm.
(2)现有110块花岗石板切割后恰好拼成若干个图②所示的正方形,并将这些正方形铺设成图③的道路,能铺设多少米?
(3)现有a张花岗石板,用方案甲切割;b张花岗石板,用方案乙切割,同时从外地材料公司调来M型小花岗石板64块.用完现有的M型和N型小花岗石板恰好能完整拼成如图③的道路图案,若61≤a≤69,则道路最多能铺设多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
(1)求证:BD是⊙O的切线;
(2)若AB=12,DB=5,求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图①,在直角三角形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,可知
,可知![]() (不需要证明);
(不需要证明);
(1)探究:如图②,![]() ,射线
,射线![]() 在这个角的内部,点
在这个角的内部,点![]() 、
、![]() 在
在![]() 的边
的边![]() 、
、![]() 上,且
上,且![]() ,
,![]() 于点
于点![]() ,
,![]() 于点
于点![]() .证明:
.证明:![]() ;
;
(2)证明:如图③,点![]() 、
、![]() 在
在![]() 的边
的边![]() 、
、![]() 上,点
上,点![]() 、
、![]() 在
在![]() 内部的射线
内部的射线![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的外角。已知
的外角。已知![]() ,
,![]() .求证:
.求证:![]() ;
;
(3)应用:如图④,在![]() 中,
中,![]() ,
,![]() .点
.点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 、
、![]() 在线段
在线段![]() 上,
上,![]() .若
.若![]() 的面积为15,则
的面积为15,则![]() 与
与![]() 的面积之和为________.
的面积之和为________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com