
【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
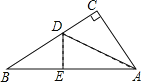
A. 3cmB. 4cmC. 5cmD. 6cm
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,E、F分别是AD和BC上的两点,EF将四边形ABCD分成两个边长为5cm的正方形,∠DEF=∠EFB=∠B=∠D=90°;点H是CD上一点且CH=lcm,点P从点H出发,沿HD以lcm/s的速度运动,同时点Q从点A出发,沿A→B→C以5cm/s的速度运动.任意一点先到达终点即停止运动;连结EP、EQ.

(1)如图1,点Q在AB上运动,连结QF,当t= 时,QF//EP;
(2)如图2,若QE⊥EP,求出t的值;
(3)试探究:当t为何值时,![]() 的面积等于
的面积等于![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形OABC摆放在平面直角坐标系中,点A在x轴上,点C在y轴上,OA=3,OC=2,过点A的直线交矩形OABC的边BC于点P,且点P不与点B、C重合,过点P作∠CPD=∠APB,PD交x轴于点D,交y轴于点E.
(1)若△APD为等腰直角三角形.
①求直线AP的函数解析式;
②在x轴上另有一点G的坐标为(2,0),请在直线AP和y轴上分别找一点M、N,使△GMN的周长最小,并求出此时点N的坐标和△GMN周长的最小值.
(2)如图2,过点E作EF∥AP交x轴于点F,若以A、P、E、F为顶点的四边形是平行四边形,求直线PE的解析式.
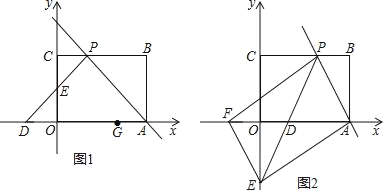
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线 AB∥CD,直线 a 分别交 AB、CD 于点 E、F,点 M 在线段 EF 上,点 P 是 直线 CD 上的一个动点(点 P 不与点 F 重合).
(1)如图 1,当点 P 在射线 FC 上移动时,∠FMP+∠FPM 与∠AEF 有什么数量关系? 请说明理由;
(2)如图 2,当点 P 在射线 FD 上移动时,∠FMP+∠FPM 与∠AEF 有什么数量关系? 请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,O 是△ABC 所在平面内的一点,连接 OB、OC,将∠ABO、∠ACO分别记为∠1、∠2.
(1)如图(1),当点 O 在图中所示的位置时,∠1+∠2+∠A+∠O= ;
(2)如图(2),当点 O 在△ABC 的内部时,∠1、∠2、∠A、∠OC四个角之间满足怎样 的数量关系?请写出你的结论并说明理由;
(3)当点 O 在△ABC 所在平面内运动时(点 O 不在三边所在的直线上),由于所处的位 置不同,∠1、∠2、∠A、∠OC四个角之间满足的数量关系还存在着与(1)、(2) 中不同的结论,请在图(3)中画出一种不同的示意图,并直接写出相应的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
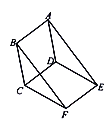
【题目】如图,已知平行四边形ABCD与平行四边形DCFE的周长相等,且![]() BAD=60°,
BAD=60°,![]() CFE=110°,则下列结论:①四边形ABFE为平行四边形;②
CFE=110°,则下列结论:①四边形ABFE为平行四边形;②![]() ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④
ADE是等腰三角形;③平行四边形ABCD与平行四边形DCFE全等;④![]() DAE=25°.其中正确的结论是.__________(填正确结论的序号)
DAE=25°.其中正确的结论是.__________(填正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB⊥BC于点B,CD⊥BC于点C,AB=4,CD=6,BC=14,P为BC边上一点,试问BP为何值时,以A,B,P为顶点的三角形与以P,C,D为顶点的三角形相似?
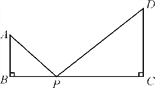
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直角三角板![]() 和直角三角板
和直角三角板![]() ,
,![]() ,
,![]() ,
,
![]() .
.
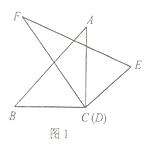
(1)如图1,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 平分
平分![]() 时,求
时,求![]() 的度数;
的度数;
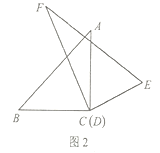
(2)在(1)的条件下,继续旋转三角板![]() ,猜想
,猜想![]() 与
与![]() 有怎样的数量关系?并利用图2所给的情形说明理由;
有怎样的数量关系?并利用图2所给的情形说明理由;
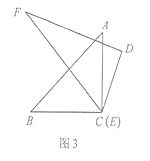
(3)如图3,将顶点![]() 和顶点
和顶点![]() 重合,保持三角板
重合,保持三角板![]() 不动,将三角板
不动,将三角板![]() 绕点
绕点![]() 旋转.当
旋转.当![]() 落在
落在![]() 内部时,直接写出
内部时,直接写出![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com