
【题目】已知△ABC,O 是△ABC 所在平面内的一点,连接 OB、OC,将∠ABO、∠ACO分别记为∠1、∠2.
(1)如图(1),当点 O 在图中所示的位置时,∠1+∠2+∠A+∠O= ;
(2)如图(2),当点 O 在△ABC 的内部时,∠1、∠2、∠A、∠OC四个角之间满足怎样 的数量关系?请写出你的结论并说明理由;
(3)当点 O 在△ABC 所在平面内运动时(点 O 不在三边所在的直线上),由于所处的位 置不同,∠1、∠2、∠A、∠OC四个角之间满足的数量关系还存在着与(1)、(2) 中不同的结论,请在图(3)中画出一种不同的示意图,并直接写出相应的结论.

【答案】(1)360°;(2)∠O=∠1+∠2+∠A;(3)∠A=∠2+∠O-∠1;
【解析】
(1)根据四边形内角和定理解答即可;
(2)连接OA,并延长交BC于D点,根据三角形内角与外角的性质解答即可;
(3)根据题意画出图形,再写出结论.
 (1)如图(1),当点O与点A在直线BC的异侧时,
(1)如图(1),当点O与点A在直线BC的异侧时,
∵AB、OB、OC、AC四条线段正好构成四边形,
∴∠1+∠2+∠A+∠O=360;
(2)连接OA,并延长交BC于D点,
∵∠BOD是△AOB的外角,
∴∠OAB+∠1=∠BOD,
∵∠COD是△AOB的外角,
∴∠OAC+∠2=∠COD,
∴∠OAB+∠1+∠OAC+∠2=∠COD+∠BOD,
即∠1+∠2+∠A=∠O.
(3)如图所示,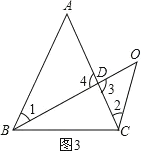
∠A=∠2+∠O∠1.
在△ABD中,∠4=180∠A∠1,
∵∠3=∠4,
∴∠3=180∠A∠1,
∴∠3+∠2+∠O=180,
∴180∠A∠1+∠2+∠O=180,
整理得,∠A=∠2+∠O∠1.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长都是1个单位长度,![]() 的顶点均在格点上.(画图要求:先用
的顶点均在格点上.(画图要求:先用![]() 铅笔画图,然后用黑色水笔描画)
铅笔画图,然后用黑色水笔描画)
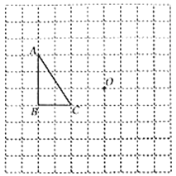
(1)①画出![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 后的
后的![]() ;
;
②连结![]() ,请判断
,请判断![]() 是怎样的三角形,并简要说明理由.
是怎样的三角形,并简要说明理由.
(2)画出![]() ,使
,使![]() 和
和![]() 关于点
关于点![]() 成中心对称;
成中心对称;
(3)请指出如何平移![]() ,使得
,使得![]() 和
和![]() 能拼成一个长方形.
能拼成一个长方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为______.
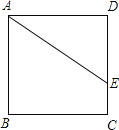
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生带手机上学的现象越来越受到社会的关注.某市记者随机调查了一些家长对这种现象的态度(A:无所谓;B:反对;C:赞成),并将调査结果绘制成图①和图②的统计图(不完整).
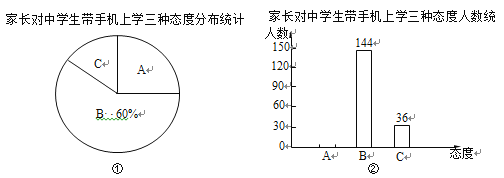
请根据图中提供的信息,解答下列问题:
(1)在图①中,C部分所占扇形的圆心角度数为___________°;选择图①进行统计的优点是___________;
(2)将图②补充完整;
(3)根据抽样调查结果,可估计该市50000名中学生家长中有_________名家长持赞成态度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,则CD等于( )
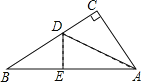
A. 3cmB. 4cmC. 5cmD. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形纸片ABCD折叠,使点D落在边AB上的D'处,点C落在C'处,若∠AD'M=50°,则∠MNC'的度数为( )

A. 100°B. 110°C. 120°D. 130°
查看答案和解析>>
科目:初中数学 来源: 题型:
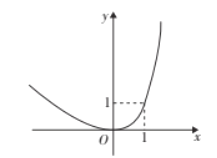
【题目】对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如:下图中的函数有0,1两个不变值,其不变长度q等于1.
(1)分别判断函数y=x-1,y=x-1,y=x2有没有不变值?如果有,直接写出其不变长度;
(2)函数y=2x2-bx.
①若其不变长度为零,求b的值;
②若1≤b≤3,求其不变长度q的取值范围;
(3) 记函数y=x2-2x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,函数G的图象由G1和G2两部分组成,若其不变长度q满足0≤q≤3,则m的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
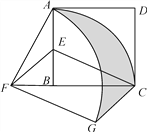
【题目】如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连结EF、CG.
(1)求证:EF∥CG;
(2)求点C、点A在旋转过程中形成的![]() 、
、![]() 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com