
【题目】如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连结EF、CG.
(1)求证:EF∥CG;
(2)求点C、点A在旋转过程中形成的![]() 、
、![]() 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.
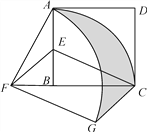
【答案】(1)证明见解析;(2) S阴影=![]() .
.
【解析】试题分析:(1)根据正方形的性质可得AB=BC=AD=2,∠ABC=90°,再根据旋转变化只改变图形的位置不改变图形的形状可得△ABF和△CBE全等,根据全等三角形对应角相等可得∠FAB=∠ECB,∠ABF=∠CBE=90°,全等三角形对应边相等可得AF=EC,然后求出∠AFB+∠FAB=90°,再求出∠CFG=∠FAB=∠ECB,根据内错角相等,两直线平行可得EC∥FG,再根据一组对边平行且相等的四边形是平行四边形判断出四边形EFGC是平行四边形,然后根据平行四边形的对边平行证明;
(2)求出FE、BE的长,再利用勾股定理列式求出AF的长,根据平行四边形的性质可得△FEC和△CGF全等,从而得到S△FEC=S△CGF,再根据S阴影=S扇形BAC+S△ABF+S△FGC﹣S扇形FAG列式计算即可得解.
试题解析:(1)证明:在正方形ABCD中,AB=BC=AD=2,∠ABC=90°.∵△BEC绕点B逆时针旋转90°得到△ABF,∴△ABF≌△CBE,∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=CE,∴∠AFB+∠FAB=90°.∵线段AF绕点F顺时针旋转90°得线段FG,∴∠AFB+∠CFG=∠AFG=90°,∴∠CFG=∠FAB=∠ECB,∴EC∥FG.∵AF=CE,AF=FG,∴EC=FG,∴四边形EFGC是平行四边形,∴EF∥CG;
(2)解:∵AD=2,E是AB的中点,∴BF=BE=![]() AB=
AB=![]() ×2=1,∴AF=
×2=1,∴AF=![]() =
=![]() =
=![]() ,由平行四边形的性质,△FEC≌△CGF,∴S△FEC=S△CGF,∴S阴影=S扇形BAC+S△ABF+S△FGC﹣S扇形FAG=
,由平行四边形的性质,△FEC≌△CGF,∴S△FEC=S△CGF,∴S阴影=S扇形BAC+S△ABF+S△FGC﹣S扇形FAG=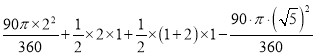
=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知△ABC,O 是△ABC 所在平面内的一点,连接 OB、OC,将∠ABO、∠ACO分别记为∠1、∠2.
(1)如图(1),当点 O 在图中所示的位置时,∠1+∠2+∠A+∠O= ;
(2)如图(2),当点 O 在△ABC 的内部时,∠1、∠2、∠A、∠OC四个角之间满足怎样 的数量关系?请写出你的结论并说明理由;
(3)当点 O 在△ABC 所在平面内运动时(点 O 不在三边所在的直线上),由于所处的位 置不同,∠1、∠2、∠A、∠OC四个角之间满足的数量关系还存在着与(1)、(2) 中不同的结论,请在图(3)中画出一种不同的示意图,并直接写出相应的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,甲车到达C地后因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地.甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图2,结合图象信息解答下列问题:
(1)乙车的速度是 千米/时,乙车行驶的时间t= 小时;
(2)求甲车从C地按原路原速返回A地的过程中,甲车距它出发地的路程y与它出发的时间x的函数关系式;
(3)直接写出甲车出发多长时间两车相距80千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
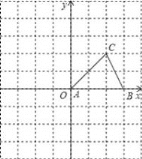
【题目】如图,△ABC的顶点A在原点,B、C坐标分别为B(3,0),C(2,2),将△ABC向左平移1个单位后再向下平移2单位,可得到△A′B′C′.
(1)请画出平移后的△A′B′C′的图形;
(2)写出△A′B′C′各个顶点的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.

(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
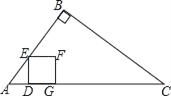
【题目】如图,在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点D从点A出发以1cm/s的速度运动到点C停止.作DE⊥AC交边AB或BC于点E,以DE为边向右作正方形DEFG.设点D的运动时间为t(s).
(1)求AC的长.
(2)请用含t的代数式表示线段DE的长.
(3)当点F在边BC上时,求t的值.
(4)设正方形DEFG与△ABC重叠部分图形的面积为S(cm2),当重叠部分图形为四边形时,求S与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
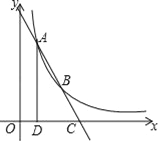
【题目】如图,点A(1,4)、B(2,a)在函数y=![]() (x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(x>0)的图象上,直线AB与x轴相交于点C,AD⊥x轴于点D.
(1)m= ;
(2)求点C的坐标;
(3)在x轴上是否存在点E,使以A、B、E为顶点的三角形与△ACD相似?若存在,求出点E的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】沙坪坝区2017年已经成功创建国家卫生城区,现在正全力争创全国文明城区(简称“创文”),某街道积极响应“创文”活动,投入一定资金用于绿化一块闲置空地,购买了甲、乙两种树木共72棵,其中甲种树木每棵90元,乙种树木每棵80元,共用去资金6160元.
(1)求甲、乙两种树木各购买了多少棵?
(2)经过一段时间后,种植的这批树木成活率高,绿化效果好,该街道决定再购买一批这两种树木绿化另一块闲置空地,两种树木的购买数量均与第一批相同,购买时发现甲种树木单价上涨了![]() ,乙种树木单价下降了
,乙种树木单价下降了![]() ,且总费用不超过6804元,求
,且总费用不超过6804元,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com