
【题目】解不等式(组)或方程(组):
(1)![]() (2)
(2)![]()
(3)(x-5)(x+4)=10;(4)![]() .
.
【答案】(1)不等式组的解集为3≤x<5;(2)![]() ;(3)x1=-5,x2=6;(4)x=3是原分式方程的根.
;(3)x1=-5,x2=6;(4)x=3是原分式方程的根.
【解析】试题分析:(1)分别解两个不等式,求出它们的解集,然后找出两个解集的公共部分即可;(2)用加减消元法求解即可;(3)整理成一元二次方程的一般形式,然后用因式分解法求解;(4)两边都乘以![]() ,把分式方程化成整式方程求解,解分式方程要验根.
,把分式方程化成整式方程求解,解分式方程要验根.
解:(1)解不等式①,得x≥3.解不等式②,得x<5.∴不等式组的解集为3≤x<5.
(2)①+②,得4x=20,即x=5.将x=5代入①,得y=1,故![]()
(3)去括号、移项、整理,得x2-x-30=0,解得x1=-5,x2=6.
(4)去分母,得1-3(x-2)=-(x-1),整理,得-2x+6=0,解得x=3.经检验,x=3是原分式方程的根.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】请认真阅读,回答下面问题:如图,![]() 为
为![]() 的中线,
的中线,![]() 与
与![]() 相等吗?(友情提示:
相等吗?(友情提示:![]() 表示三角形面积)
表示三角形面积)
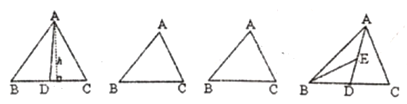
解:过![]() 点作
点作![]() 边上的高
边上的高![]() ,
,
∵![]() 为
为![]() 的中线
的中线
∴![]()
∵![]()
![]()
∴![]()
(1)用一句简洁的文字表示上面这段内容的结论;
(2)利用上面所得的结论,用不同的割法分别把下面两个三角形面积4等分,(只要割线不同就算一种)
(3)已知:![]() 为
为![]() 的中线,点
的中线,点![]() 为
为![]() 边上的中点,若
边上的中点,若![]() 的面积为20,
的面积为20,![]() ,求点
,求点![]() 到
到![]() 边的距离为多少?
边的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
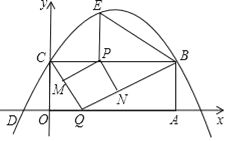
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
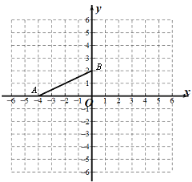
【题目】如图,在平面直角坐标系中,已知点A(-4,0)、B(0,2),点P(a,a).
(1)当a=2时,将△AOB绕点P(a,a)逆时针旋转90°得△DEF,点A的对应点为D,点O的对应点为E,点B的对应点为点F,在平面直角坐标系中画出△DEF,并写出点D的坐标 ;
(2)作线段AB关于P点的中心对称图形(点A、B的对应点分别是G、H),若四边形ABGH是正方形,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年12月4日是第五个国家宪法日,也是第一个“宪法宣传周”.甲、乙两班各选派10名学生参加宪法知识竞赛(满分100分),成绩如下:
成绩 | 85 | 90 | 95 | 100 |
甲班参赛学生/人 | 1 | 1 | 5 | 3 |
乙班参赛学生/人 | 1 | 2 | 3 | 4 |
分别求甲、乙两班参赛学生竞赛成绩的平均数和方差.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是AD和BC上的两点,EF将四边形ABCD分成两个边长为5cm的正方形,∠DEF=∠EFB=∠B=∠D=90°;点H是CD上一点且CH=lcm,点P从点H出发,沿HD以lcm/s的速度运动,同时点Q从点A出发,沿A→B→C以5cm/s的速度运动.任意一点先到达终点即停止运动;连结EP、EQ.

(1)如图1,点Q在AB上运动,连结QF,当t= 时,QF//EP;
(2)如图2,若QE⊥EP,求出t的值;
(3)试探究:当t为何值时,![]() 的面积等于
的面积等于![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
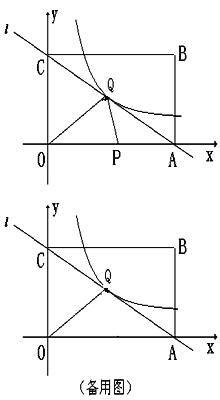
【题目】已知,长方形OABC在平面直角坐标系内的位置如图所示,点O为坐标原点,点A的坐标为(10,0),点B的坐标为(10,8).
(1)直接写出点C的坐标为:C( , );
(2)已知直线AC与双曲线y=![]() (m≠0)在第一象限内有一点交点Q为(5,n);
(m≠0)在第一象限内有一点交点Q为(5,n);
①求m及n的值;
②若动点P从A点出发,沿折线AO→OC的路径以每秒2个单位长度的速度运动,到达C处停止.求△OPQ的面积S与点P的运动时间t(秒)的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
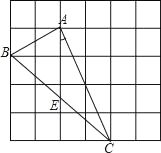
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
请按要求完成下列各题:
(1)用2B铅笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 ;
(4)若E为BC中点,则tan∠CAE的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,O 是△ABC 所在平面内的一点,连接 OB、OC,将∠ABO、∠ACO分别记为∠1、∠2.
(1)如图(1),当点 O 在图中所示的位置时,∠1+∠2+∠A+∠O= ;
(2)如图(2),当点 O 在△ABC 的内部时,∠1、∠2、∠A、∠OC四个角之间满足怎样 的数量关系?请写出你的结论并说明理由;
(3)当点 O 在△ABC 所在平面内运动时(点 O 不在三边所在的直线上),由于所处的位 置不同,∠1、∠2、∠A、∠OC四个角之间满足的数量关系还存在着与(1)、(2) 中不同的结论,请在图(3)中画出一种不同的示意图,并直接写出相应的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com