
【题目】请认真阅读,回答下面问题:如图,![]() 为
为![]() 的中线,
的中线,![]() 与
与![]() 相等吗?(友情提示:
相等吗?(友情提示:![]() 表示三角形面积)
表示三角形面积)
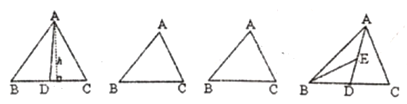
解:过![]() 点作
点作![]() 边上的高
边上的高![]() ,
,
∵![]() 为
为![]() 的中线
的中线
∴![]()
∵![]()
![]()
∴![]()
(1)用一句简洁的文字表示上面这段内容的结论;
(2)利用上面所得的结论,用不同的割法分别把下面两个三角形面积4等分,(只要割线不同就算一种)
(3)已知:![]() 为
为![]() 的中线,点
的中线,点![]() 为
为![]() 边上的中点,若
边上的中点,若![]() 的面积为20,
的面积为20,![]() ,求点
,求点![]() 到
到![]() 边的距离为多少?
边的距离为多少?
【答案】(1)三角形中线平分三角形的面积;或等底同高的三角形,面积相等;(2)![]() ;(3)2.5
;(3)2.5
【解析】
(1)根据推导过程,知三角形中线平分三角形的面积;
(2)根据(1)的结论,先做出△ABC的一条中线AD,然后再分别作出△ABD和△ACD的一条中线即可;
(3)根据(1)的结论求得△BED的面积,进一步根据三角形的面积公式求解.
解:(1)三角形中线平分三角形的面积.
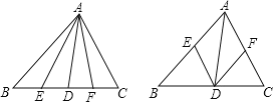
(2)第一种方法:BE=DE=DF=CF;
第二种方法:BD=CD,AE=BE,AF=CF.
(3))∵AD为△ABC的中线,点E为AD边上的中点,若△ABC的面积为20,
∴S△BDE的面积=![]() S△ABC=5.
S△ABC=5.
又BD=4,
则点E到BC边的距离是2.5.


 优加精卷系列答案
优加精卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△P1OA1,△P2A1A2,△P3A2A3,…都是等腰直角三角形,其直角顶点P1(3,3),P2,P3,…均在直线y=﹣![]() x+4上,设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…依据图形所反映的规律,S2019=_____.
x+4上,设△P1OA1,△P2A1A2,△P3A2A3,…的面积分别为S1,S2,S3,…依据图形所反映的规律,S2019=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
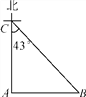
【题目】如图,海面上B,C两岛分别位于A岛的正东和正北方向.一艘船从A岛出发,以18海里/时的速度向正北方向航行2小时到达C岛,此时测得B岛在C岛的南偏东43°.求A,B两岛之间的距离.(结果精确到0.1海里)(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)
查看答案和解析>>
科目:初中数学 来源: 题型:
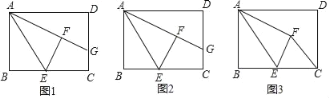
【题目】如图,在矩形ABCD中,E是BC上一动点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,AB=3,AD=4.
(1)如图,当∠DAG=30° 时,求BE的长;
(2)如图,当点E是BC的中点时,求线段GC的长;
(3)如图,点E在运动过程中,当△CFE的周长最小时,直接写出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.

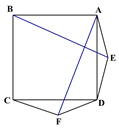

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.
(1)为了求得剩余草坪的面积,小明同学想出了两种办法,结果分别如下:
方法①: 方法②:
请你从小明的两种求面积的方法中,直接写出含有字母a,b代数式的等式是:
(2)根据(1)中的等式,解决如下问题:
①已知:![]() ,求
,求![]() 的值;
的值;
②己知:![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com