
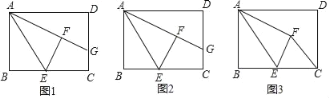
【题目】如图,在矩形ABCD中,E是BC上一动点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,AB=3,AD=4.
(1)如图,当∠DAG=30° 时,求BE的长;
(2)如图,当点E是BC的中点时,求线段GC的长;
(3)如图,点E在运动过程中,当△CFE的周长最小时,直接写出BE的长.
【答案】(1)∵四边形ABCD是矩形,
∴∠BAD=90,
∵∠DAG=30,
∴∠BAG=60
由折叠知,∠BAE=![]() ∠BAG=30,
∠BAG=30,
在Rt△BAE中,∠BAE=30,AB=3,
∴BE=![]()
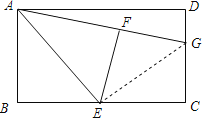
(2)如图,连接GE,
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90,
∴∠EFG=90,
∵在Rt△GFE和Rt△GCE中,
EG=EG,
EF=EC,
∴Rt△GFE≌Rt△GCE(HL),
∴GF=GC;
设GC=x,则AG=3+x,DG=3x,
在Rt△ADG中,42+(3x)2=(3+x)2,
解得x=![]() .
.
(3)如图1,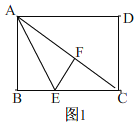
由折叠知,∠AFE=∠B=90,EF=BE,
∴EF+CE=BE+CE=BC=AD=4,
∴当CF最小时,△CEF的周长最小,
∵∠AFE=90,
∴点A,F,C在同一条直线上时,CF最小,
由折叠知,AF=AB=3,
在Rt△ABC中,AB=3,BC=AD=4,
∴AC=5,
∴CF=ACAF=2,
在Rt△CEF中,
.EF2+CF2=CE2,
∴BE2+CF2=(4BE)2,
∴BE2+22=(4BE)2,
∴BE=![]() .
.
【解析】
试题(1)先确定出∠BAE=30°,再利用含30°的直角三角形的性质即可得出结论
(2)连接GE,根据点E是BC的中点以及翻折的性质可以求出BE=EF=EC,然后利用“HL”证明△GFE和△GCE全等,根据全等三角形对应边相等即可得证FG=CG,设GC=x,表示出AG、DG,然后在Rt△ADG中,利用勾股定理列式进行计算即可得解;
(3)先判断出EF⊥AC时,△CEF的周长最小,最后用勾股定理即可得出结论.
试题解析:(1)∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠DAG=30°,
∴∠BAG=60°
由折叠知,∠BAE=![]() ∠BAG=30°,
∠BAG=30°,
在Rt△BAE中,∠BAE=30°,AB=3,
∴BE=![]() ;
;
(2)如图,/span>连接GE,
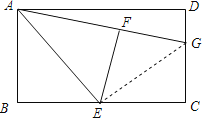
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90°,
∴∠EFG=90°,
∵在Rt△GFE和Rt△GCE中,![]() ,
,
∴Rt△GFE≌Rt△GCE(HL),
∴GF=GC;
设GC=x,则AG=3+x,DG=3x,
在Rt△ADG中,42+(3x)2=(3+x)2,
解得x=![]() .
.
(3)如图1,
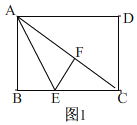
由折叠知,∠AFE=∠B=90°,EF=BE,
∴EF+CE=BE+CE=BC=AD=4,
∴当CF最小时,△CEF的周长最小,
∵∠AFE=90°,
∴点A,F,C在同一条直线上时,CF最小,
由折叠知,AF=AB=3,
在Rt△ABC中,AB=3,BC=AD=4,
∴AC=5,
∴CF=ACAF=2,
在Rt△CEF中,EF2+CF2=CE2,
∴BE2+CF2=(4BE)2,
∴BE2+22=(4BE)2,
∴BE=![]() .
.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?

查看答案和解析>>
科目:初中数学 来源: 题型:
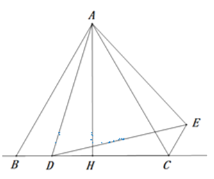
【题目】如图,在![]() 中,
中,![]() ,
,![]() 垂足为
垂足为![]() ,
,![]() 为直线
为直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),在
重合),在![]() 的右侧作
的右侧作![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 在线段
在线段![]() 上时
上时
① 求证:![]() ≌
≌![]() ;
;
② 若![]() , 则
, 则![]() ;
;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一农民朋友带了若干千克的土豆进城出售,为了方便,他带了一些零钱备用.按市场售出一些后,又降价出售.售出土豆千克数![]() 与他手中持有的钱数
与他手中持有的钱数![]() (含备用零钱)的关系如图所示,结合图像回答下列问题:
(含备用零钱)的关系如图所示,结合图像回答下列问题:
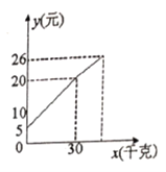
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余的土豆售完,这时他手中的钱(含备用的钱)是26元,问他一共带了多少千克的土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读,回答下面问题:如图,![]() 为
为![]() 的中线,
的中线,![]() 与
与![]() 相等吗?(友情提示:
相等吗?(友情提示:![]() 表示三角形面积)
表示三角形面积)
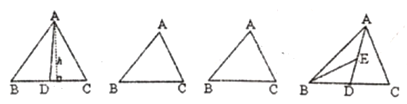
解:过![]() 点作
点作![]() 边上的高
边上的高![]() ,
,
∵![]() 为
为![]() 的中线
的中线
∴![]()
∵![]()
![]()
∴![]()
(1)用一句简洁的文字表示上面这段内容的结论;
(2)利用上面所得的结论,用不同的割法分别把下面两个三角形面积4等分,(只要割线不同就算一种)
(3)已知:![]() 为
为![]() 的中线,点
的中线,点![]() 为
为![]() 边上的中点,若
边上的中点,若![]() 的面积为20,
的面积为20,![]() ,求点
,求点![]() 到
到![]() 边的距离为多少?
边的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
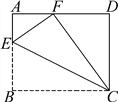
【题目】如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
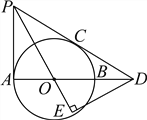
【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A、C,PC交AB的延长线于点D.DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA=![]() ,求OE的长.
,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
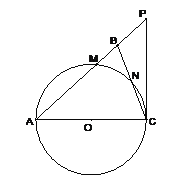
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是AD和BC上的两点,EF将四边形ABCD分成两个边长为5cm的正方形,∠DEF=∠EFB=∠B=∠D=90°;点H是CD上一点且CH=lcm,点P从点H出发,沿HD以lcm/s的速度运动,同时点Q从点A出发,沿A→B→C以5cm/s的速度运动.任意一点先到达终点即停止运动;连结EP、EQ.

(1)如图1,点Q在AB上运动,连结QF,当t= 时,QF//EP;
(2)如图2,若QE⊥EP,求出t的值;
(3)试探究:当t为何值时,![]() 的面积等于
的面积等于![]() 面积的
面积的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com