
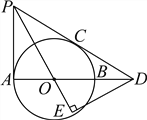
【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A、C,PC交AB的延长线于点D.DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA=![]() ,求OE的长.
,求OE的长.
【答案】(1)证明见解析;(2) OE=![]() .
.
【解析】试题分析:(1)根据切线长定理和切线的性质即可证明:∠EPD=∠EDO;
(2)连接OC,利用tan∠PDA=![]() ,可求出CD=4,再证明△OED∽△DEP,根据相似三角形的性质和勾股定理即可求出OE的长.
,可求出CD=4,再证明△OED∽△DEP,根据相似三角形的性质和勾股定理即可求出OE的长.
试题解析:(1)证明:PA,PC与⊙O分别相切于点A,C,
∴∠APO=∠EPD且PA⊥AO,
∴∠PAO=90°,
∵∠AOP=∠EOD,∠PAO=∠E=90°,
∴∠APO=∠EDO,
∴∠EPD=∠EDO;
(2)解:连接OC,
∴PA=PC=6,
∵tan∠PDA=![]() ,
,
∴在Rt△PAD中,AD=8,PD=10,
∴CD=4,
∵tan∠PDA=![]() ,
,
∴在Rt△OCD中,OC=OA=3,OD=5,
∵∠EPD=∠ODE,
∴△OED∽△DEP,
∴![]() ,
,
∴DE=2OE
在Rt△OED中,OE2+DE2=OD2,即5OE2=52,
∴OE=![]() .
.


科目:初中数学 来源: 题型:
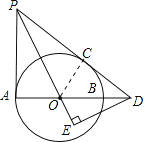
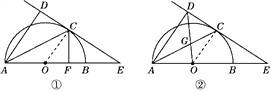
【题目】如图①,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图②,连接OD交AC于点G,若![]() ,求sinE的值.
,求sinE的值.

【答案】(1)证明见解析;(2)CF=![]() ;(3) sinE=
;(3) sinE=![]() .
.
【解析】分析:(1)连接OC,由平行线的判定定理、性质以及三角形中的等角对等边的原理即可求证。(2)由(1)中结论,利用特殊角的三角函数值可求出∠E=30和CF的长度。(3)连接OC,即可证得△OCG∽△DAG,△OCE∽△DAE,根据相似三角形的对应边成比例,可得EO与AO的比例关系,又因为OC=OA,所以在RT△OCE中由三角函数的定义即可求解。
本题解析:(1)连接OC,如图①.∵OC切半圆O于C,∴OC⊥DC,又AD⊥CD.∴OC∥AD.∴∠OCA=∠DAC.∵OC=OA,∴∠OAC=∠ACO.∴∠DAC=∠CAO,即AC平分∠DAB.
(2)在Rt△OCE中,∵OC=OB=![]() OE,∴∠E=30°.
OE,∴∠E=30°.
∴在Rt△OCF中,CF=OC·sin60°=2×![]() =
=![]() .
.
(3)连接OC,如图②.∵CO∥AD,∴△CGO∽△AGD.∴![]() =
=![]() =
=![]() .不妨设CO=AO=3k,则AD=4k.又△COE∽△DAE,∴
.不妨设CO=AO=3k,则AD=4k.又△COE∽△DAE,∴![]() =
=![]() =
=![]() =
=![]() .∴EO=9k.在Rt△COE中,sinE=
.∴EO=9k.在Rt△COE中,sinE=![]() =
=![]() =
=![]() .
.
【题型】解答题
【结束】
25
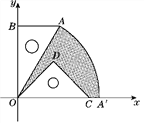
【题目】如图,有一块含30°角的直角三角板OAB的直角边BO的长恰与另一块等腰直角三角板ODC的斜边OC的长相等,把这两块三角板放置在平面直角坐标系中,且OB=3![]() .
.
(1)若某反比例函数的图象的一个分支恰好经过点A,求这个反比例函数的解析式;
(2)若把含30°角的直角三角板绕点O按顺时针方向旋转后,斜边OA恰好落在x轴上,点A落在点A′处,试求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
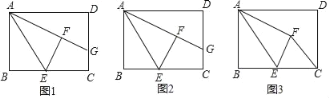
【题目】如图,在矩形ABCD中,E是BC上一动点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G,AB=3,AD=4.
(1)如图,当∠DAG=30° 时,求BE的长;
(2)如图,当点E是BC的中点时,求线段GC的长;
(3)如图,点E在运动过程中,当△CFE的周长最小时,直接写出BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在正方形ABCD的外侧作两个等边三角形ADE和DCF,连接AF,BE.

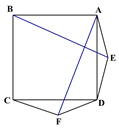

(图1) (图2) (备用图)
(1)请判断:AF与BE的数量关系是_____________,位置关系______________;
(2)如图2,若将条件“两个等边三角形ADE和DCF”变为“两个等腰三角形ADE和DCF,且EA=ED=FD=FC”,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
(3)若三角形ADE和DCF为一般三角形,且AE=DF,ED=FC,第(1)问中的结论都能成立吗?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
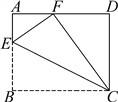
【题目】如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处,若AB=4,BC=5,则tan∠AFE的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.
(1)为了求得剩余草坪的面积,小明同学想出了两种办法,结果分别如下:
方法①: 方法②:
请你从小明的两种求面积的方法中,直接写出含有字母a,b代数式的等式是:
(2)根据(1)中的等式,解决如下问题:
①已知:![]() ,求
,求![]() 的值;
的值;
②己知:![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年农历五月初五,是中国民间的传统节日——端午节.它始于我国的春秋战国时期,已列为世界非物质文化遗产.时至今日,端午节在我国仍是一个十分盛行的节日.今年端午节,某地甲、乙两家超市为吸引更多的顾客,开展促销活动,对某种质量和售价相同的粽子分别推出了不同的优惠方案.甲超市的方案是:购买该种粽子超过80元后,超出80元的部分按九折收费;乙超市的方案是:购买该种粽子超过120元后,超出120元的部分按八折收费.请根据顾客购买粽子的金额,选择到哪家超市购买粽子划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为( )

A. 12B. 14C. 16D. 18
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com