
【题目】如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.
(1)为了求得剩余草坪的面积,小明同学想出了两种办法,结果分别如下:
方法①: 方法②:
请你从小明的两种求面积的方法中,直接写出含有字母a,b代数式的等式是:
(2)根据(1)中的等式,解决如下问题:
①已知:![]() ,求
,求![]() 的值;
的值;
②己知:![]() ,求
,求![]() 的值.
的值.

【答案】(1)(a-b)2;a2-2ab+b2;(a-b)2=a2-2ab+b2;(2)ab=-2.5;(x-2019)2=5.
【解析】
(1)方法①是根据已知条件先表示出矩形的长和宽,再根据矩形的面积公式即可得出答案;方法②是正方形的面积减去两条道路的面积,即可得出剩余草坪的面积;根据(1)得出的结论可得出![]() ;
;
(2)①分别把![]() 的值和
的值和![]() 的值代入(1)中等式,即可得到答案;
的值代入(1)中等式,即可得到答案;
②根据题意,把(x-2018)和(x-2020)变成(x-2019)的形式,然后计算完全平方公式,展开后即可得到答案.
解:(1)方法①:草坪的面积=(a-b)(a-b)=![]() .
.
方法②:草坪的面积=![]() ;
;
等式为:![]()
故答案为:![]() ,
,![]() ;
;![]()
(2)①把![]() 代入
代入![]()
∴![]() ,
,
∴![]()
②原式可化为:![]()
∴![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】2013年3月28日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计,请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:


频率分布表 频数分布直方图
(1)这次抽取了名学生的竞赛成绩进行统计,其中: ![]() ,
, ![]() ;
;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读,回答下面问题:如图,![]() 为
为![]() 的中线,
的中线,![]() 与
与![]() 相等吗?(友情提示:
相等吗?(友情提示:![]() 表示三角形面积)
表示三角形面积)
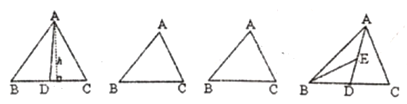
解:过![]() 点作
点作![]() 边上的高
边上的高![]() ,
,
∵![]() 为
为![]() 的中线
的中线
∴![]()
∵![]()
![]()
∴![]()
(1)用一句简洁的文字表示上面这段内容的结论;
(2)利用上面所得的结论,用不同的割法分别把下面两个三角形面积4等分,(只要割线不同就算一种)
(3)已知:![]() 为
为![]() 的中线,点
的中线,点![]() 为
为![]() 边上的中点,若
边上的中点,若![]() 的面积为20,
的面积为20,![]() ,求点
,求点![]() 到
到![]() 边的距离为多少?
边的距离为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A、C,PC交AB的延长线于点D.DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA=![]() ,求OE的长.
,求OE的长.
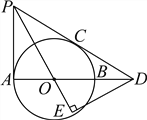
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PA、PC与⊙O分别相切于点A、C,PC交AB的延长线于点D.DE⊥PO交PO的延长线于点E.
(1)求证:∠EPD=∠EDO;
(2)若PC=6,tan∠PDA=![]() ,求OE的长.
,求OE的长.
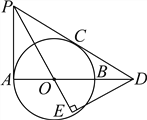
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求⊙O的半径及△ACP的周长.
,求⊙O的半径及△ACP的周长.
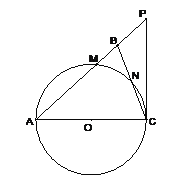
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的两边在坐标轴上,点A的坐标为(10,0),抛物线y=ax2+bx+4过点B,C两点,且与x轴的一个交点为D(﹣2,0),点P是线段CB上的动点,设CP=t(0<t<10).
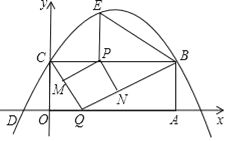
(1)请直接写出B、C两点的坐标及抛物线的解析式;
(2)过点P作PE⊥BC,交抛物线于点E,连接BE,当t为何值时,∠PBE和Rt△OCD中的一个角相等?
(3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N,当四边形PMQN为正方形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
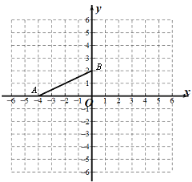
【题目】如图,在平面直角坐标系中,已知点A(-4,0)、B(0,2),点P(a,a).
(1)当a=2时,将△AOB绕点P(a,a)逆时针旋转90°得△DEF,点A的对应点为D,点O的对应点为E,点B的对应点为点F,在平面直角坐标系中画出△DEF,并写出点D的坐标 ;
(2)作线段AB关于P点的中心对称图形(点A、B的对应点分别是G、H),若四边形ABGH是正方形,则a= .
查看答案和解析>>
科目:初中数学 来源: 题型:
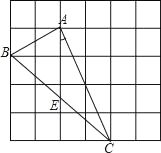
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
请按要求完成下列各题:
(1)用2B铅笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 ;
(4)若E为BC中点,则tan∠CAE的值是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com