
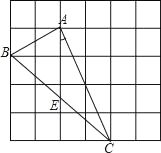
【题目】如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,
请按要求完成下列各题:
(1)用2B铅笔画AD∥BC(D为格点),连接CD;
(2)线段CD的长为 ;
(3)请你在△ACD的三个内角中任选一个锐角,若你所选的锐角是 ,则它所对应的正弦函数值是 ;
(4)若E为BC中点,则tan∠CAE的值是 .
【答案】(1)作图见解析;(2)![]() ;(3)∠CAD;
;(3)∠CAD;![]() ;或∠ADC,
;或∠ADC,![]() .
.
【解析】试题分析:(1)直接利用网格结合平行线的判定方法得出D点位置;
(2)直接利用勾股定理得出DC的长;
(3)利用勾股定理的逆定理得出△ACD是直角三角形,进而得出答案;
(4)根据直角三角形斜边上的中线等于斜边的一半得出AE=EC,可得∠ACB=∠CAE,然后在Rt△ABC中求出tan∠ACB的值即为tan∠CAE的值.
试题解析:
解:(1)如图所示:
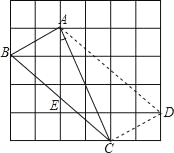
D点即为所求;
(2)DC=![]() =
=![]() ;
;
故答案为:![]() ;
;
(3)在△ACD的三个内角中所选的锐角是:∠CAD,
∵CD=![]() ,AD=5,AC=
,AD=5,AC=![]() ,
,
∴CD2+AC2=AD2,
∴△ACD是直角三角形,
∴∠CAD它所对应的正弦函数值是:![]() =
=![]() ;
;
当所选的锐角是:∠ADC,
则∠ADC它所对应的正弦函数值是:![]() =
=![]() .
.
故答案为:∠CAD,![]() 或∠ADC,
或∠ADC,![]() ;
;
(4)AB=![]() ,AC=
,AC=![]() ,BC=5,
,BC=5,
∴AB2+AC2=BC2,
∴△ABC为直角三角形,
∵E为BC中点,
∴AE=EC,
∴∠ACB=∠CAE,
∴tan∠CAE=tan∠ACB=![]() =
=![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.
(1)为了求得剩余草坪的面积,小明同学想出了两种办法,结果分别如下:
方法①: 方法②:
请你从小明的两种求面积的方法中,直接写出含有字母a,b代数式的等式是:
(2)根据(1)中的等式,解决如下问题:
①已知:![]() ,求
,求![]() 的值;
的值;
②己知:![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为( )

A. 12B. 14C. 16D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由相同的小正方形按照一定规律摆放而成,其中第1个图共有3个小正方形,第2个图共有8个小正方形,第3个图共有15个小正方形,第4个图共有24个小正方形,…,照此规律排列下去,则第8个图中小正方形的个数是( )
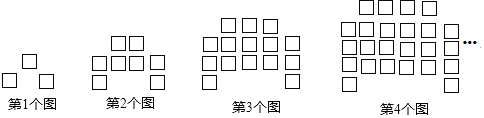
A. 48B. 63C. 80D. 99
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开设了丰富多彩的实践类拓展课程,分别设置了体育类、艺术类、文学类及其它类课程(要求人人参与,每人只能选择一门课程).为了解学生喜爱的拓展课类别,学校做了一次抽样调查.根据收集到的数据,绘制成如下两幅不完整的统计图,请根据图中提供的信息,完成下列问题:

(1)此次共调查了多少人?
(2)请将条形统计图补充完整
(3)求文学类课程在扇形统计图中所占圆心角的度数;
(4)若该校有1500名学生,请估计喜欢体育类拓展课的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长都是1个单位长度,![]() 的顶点均在格点上.(画图要求:先用
的顶点均在格点上.(画图要求:先用![]() 铅笔画图,然后用黑色水笔描画)
铅笔画图,然后用黑色水笔描画)
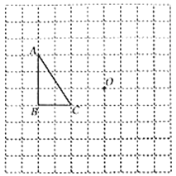
(1)①画出![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 后的
后的![]() ;
;
②连结![]() ,请判断
,请判断![]() 是怎样的三角形,并简要说明理由.
是怎样的三角形,并简要说明理由.
(2)画出![]() ,使
,使![]() 和
和![]() 关于点
关于点![]() 成中心对称;
成中心对称;
(3)请指出如何平移![]() ,使得
,使得![]() 和
和![]() 能拼成一个长方形.
能拼成一个长方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示)把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为______.
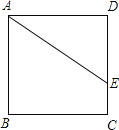
查看答案和解析>>
科目:初中数学 来源: 题型:
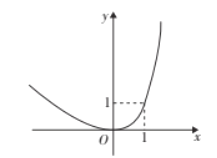
【题目】对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如:下图中的函数有0,1两个不变值,其不变长度q等于1.
(1)分别判断函数y=x-1,y=x-1,y=x2有没有不变值?如果有,直接写出其不变长度;
(2)函数y=2x2-bx.
①若其不变长度为零,求b的值;
②若1≤b≤3,求其不变长度q的取值范围;
(3) 记函数y=x2-2x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,函数G的图象由G1和G2两部分组成,若其不变长度q满足0≤q≤3,则m的取值范围为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com