
如图,在□ABCD中,E,F分别为边AB和CD的中点,连接DE,BF,且AB=2AD=4.
(1)求证:△AED≌△CFB;(4分)

(2)当四边形DEBF为菱形时,求出该菱形的面积;(4分)
(1)证明见试题解析;(2) .
.
【解析】
试题分析:(1)首先根据平行四边形的性质可得AD=BC,∠A=∠C,再加上条件AE=CF可利用SAS证明△AED≌△CFB;
(2)作FM⊥AB于M,可以得到△BFC是等边三角形,得到∠FBM=60°,再求出菱形的高FM,从而得到菱形的面积.
解答:证明:(1)∵四边形ABCD是平行四边形,∴AD=BC,∠A=∠C,
在△ADE和△CBF中,∵AD=BC,∠A=∠C,AE=CF,∴△AED≌△CFB(SAS);
(2)作FM⊥AB于M,
在菱形DEBF中,BE=BF= AB=
AB= ,∵CF=
,∵CF=  CD=
CD= ,BC=AD=
,BC=AD= AB=2,∴CF=BC=BF,∴△BFC是等边三角形,∴∠BFC=60°,∵ABCD是平行四边形,∴AB∥CD,∴∠MBF=∠BFC=60°,∴∠FBM=30°,∴MB=
AB=2,∴CF=BC=BF,∴△BFC是等边三角形,∴∠BFC=60°,∵ABCD是平行四边形,∴AB∥CD,∴∠MBF=∠BFC=60°,∴∠FBM=30°,∴MB= BF=1,∴FM=
BF=1,∴FM= MB=
MB= ,∴菱形DEBF的面积=BE•FM=
,∴菱形DEBF的面积=BE•FM= .
.
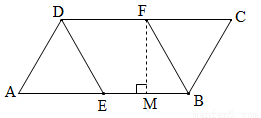
考点:1.全等三角形的判定与性质;2.平行四边形的性质.


科目:初中数学 来源:2013-2014学年江苏省九年级直升班第一次综合测试数学试卷(解析版) 题型:选择题
如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA、OB在0点钉在一起,并使它们保持垂直,在测直径时,把0点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )

A.12个单位 B.10个单位 C.4个单位 D.15个单位
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新疆阿拉尔市九年级秋季班第一次月考数学试卷(解析版) 题型:填空题
直角三角形的两直角边的比是3︰4,而斜边的长是20㎝,那么这个三角形的面积是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市海怡翠学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,直角梯形OABC,OC边放在x轴上,OA边放在y轴上,OC=12,BC=8,∠C=60°,点P以1个单位的速度从O点出发沿OC运动,点Q以相同的速度从C点出发,沿CB—BA运动,当一点到达终点时,两点停止运动;

(1)写出B点的坐标;(2分)
(2)写出△OPQ的面积S与时间t之间的函数关系式(3分)
(3)当Q点在BC边上运动时,是否存在t值,使△OPQ为等腰三角形?若有,求出此时的t 值.如果没有,请说明理由(4分)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市海怡翠学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列给出的条件中,能判断四边形ABCD是平行四边形的是( )
A.∠A=∠C,AD∥BC B.AB∥CD,AD=BC
C.∠B=∠C,∠A=∠D D.∠A=∠C,AD=BC
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省英文实验学校九年级上学期第一次月考数学试卷(解析版) 题型:填空题
在两个布袋中分别装有三个小球,这三个小球的颜色分别为红色、白色、绿色,其他没有区别.把两袋小球都搅匀后,再分别从两袋中各取出一个小球,求取出两个相同颜色小球的概率是_______。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年天津市和平区结课考试数学试卷(解析版) 题型:解答题
已知抛物线y=ax2+bx+c经过A(3,0)、B(0,3)、C(1,0)三点.
(1)求抛物线的解析式;
(2)若点D的坐标为(﹣1,0),在直线AB上有一点P,使△ABO与△ADP相似,求出点P的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上,是否存在点E,使△ADE的面积等于四边形APCE的面积?如果存在,请求出点E的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com