
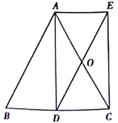
【题目】如图,AD是等腰△ABC底边BC上的高,点O是AC中点,延长DO到E
使AE∥BC,连接AE。
(1)求证:四边形ADCE是矩形;
(2)①若AB=17,BC=16,则四边形ADCE的面积= ;
②若AB=10,则BC= 时,四边形ADCE是正方形。
【答案】(1)见解析;(2)①120; ②![]() .
.
【解析】试题分析:(1)根据平行四边形的性质得出四边形ADCE是平行四边形,根据垂直推出∠ADC=90°,根据矩形的判定得出即可;
(2)①求出DC,根据勾股定理求出AD,根据矩形的面积公式求出即可;
②要使ADCE是正方形,只需要AC⊥DE,即∠DOC=90°,只需要OD2+OC2=DC2,即可得到BC的长.
试题解析:(1)证明:∵AE∥BC,∴∠AEO=∠CDO.又∵∠AOE=∠COD,OA=OC,∴△AOE≌△COD,∴OE=OD,而OA=OC,∴四边形ADCE是平行四边形.∵AD是BC边上的高,∴∠ADC=90°.∴□ADCE是矩形.
(2)①解:∵AD是等腰△ABC底边BC上的高,BC=16,AB=17,∴BD=CD=8,AB=AC=17,∠ADC=90°,由勾股定理得:AD=![]() =
=![]() =15,∴四边形ADCE的面积是AD×DC=15×8=120.
=15,∴四边形ADCE的面积是AD×DC=15×8=120.
②当BC=![]() 时,DC=DB=
时,DC=DB=![]() .∵ADCE是矩形,∴OD=OC=5.∵OD2+OC2=DC2,∴∠DOC=90°,∴AC⊥DE,∴ADCE是正方形.
.∵ADCE是矩形,∴OD=OC=5.∵OD2+OC2=DC2,∴∠DOC=90°,∴AC⊥DE,∴ADCE是正方形.


科目:初中数学 来源: 题型:
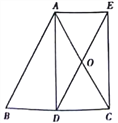
【题目】在由6个边长为1的小正方形组成的方格中:
(1)如图(1),A、B、C是三个格点(即小正方形的顶点),判断AB与BC的关系,并说明理由;
(2)如图(2),连结三格和两格的对角线,求∠α+∠β的度数(要求:画出示意图并给出证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】幻方起源于中国,传说在大禹治水时,有只神龟在洛水中浮起,龟背上有奇特的图案,如图1,人们称之为洛书.如果将龟背上的数字翻译出来,如图2.
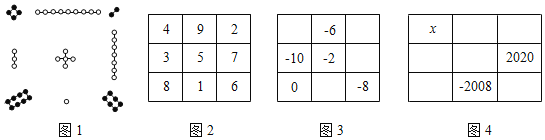
观察发现,图2的每行、每列、每条对角线的三个数之和都是15.像这样,在3×3的方阵图中,每行、每列、每条对角线上3个数的和都相等,我们就称它为三阶幻方.上面的三阶幻方中,15是这个幻方的和,简称幻和.5是幻方最中心的数字,简称中心数.
(1)用﹣10,﹣8,﹣6,﹣4,﹣2,0,2,4,6这九个数字补全图3中的幻方;
(2)如图4是一个三阶幻方,试确定图4中x的值,并给出求解过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
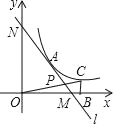
【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=![]() (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l和反比例函数的解析式;
(2)在函数y=![]() (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年3月,某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动,活动结束后,随机抽取了部分同学的成绩(x均为整数,总分100分),绘制了如下尚不完整的统计图表.
调查结果统计表
组别 | 成绩分组(单位:分) | 频数 | 频率 |
A | 80≤x<85 | 50 | 0.1 |
B | 85≤x<90 | 75 | |
C | 90≤x<95 | 150 | c |
D | 95≤x≤100 | a | |
合计 | b | 1 |
根据以上信息解答下列问题:
(1)统计表中,a=_____,b=_____,c=_____;
(2)扇形统计图中,m的值为_____,“C”所对应的圆心角的度数是_____;
(3)若参加本次竞赛的同学共有5000人,请你估计成绩在95分及以上的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为探测某座山的高度AB,某飞机在空中C处测得山顶A处的俯角为31°,此时飞机的飞行高度为CH=4千米;保持飞行高度与方向不变,继续向前飞行2千米到达D处,测得山顶A处的俯角为50°,求此山的高度AB.(参考数据:tan31°≈0.6,1an50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
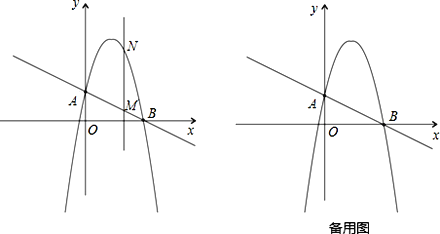
【题目】如图,一次函数![]() 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线![]() 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
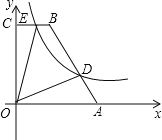
【题目】如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0), (2,6),点D为AB上一点,且BD=2AD,双曲线y=![]() (k>0)经过点D,交BC于点E.
(k>0)经过点D,交BC于点E.
(1)求双曲线的解析式;
(2)求四边形ODBE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com