【题目】如图，某人在建筑物
的顶部测得一烟囱
的顶端
的仰角为
，测得在湖中的倒影
的俯角为
，已知
，则烟囱的高为________
．
【答案】20（2+
）
【解析】
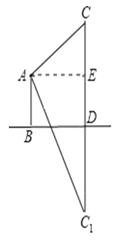
作AE⊥CD于E点，则根据矩形性质可知ED=AB=20，设CD=x，则在△AEC中，AE=EC=x﹣20；又根据平面镜成像可知C1D=CD=x，即C1E=x+20，从而在△AC1E中，借助于60°角的正切值列方程解答即可．
作AE⊥CD于E点，设CD=xm，由题意得：四边形ABDE为矩形，∴AB=ED=20，∴CE=x﹣20．在Rt△ACE中，∵∠CAE=45°，∴AE=CE=x﹣20，根据平面镜成像可知C1D=CD=x，∴C1E=x+20．在Rt△AEC1中，∵∠EAC1=60°，∴C1E=AEtan60°，即x+20=（x﹣20）
，解得：x=20（2
）．
即烟囱CD的高为20（2）m．
故答案为：20（2）．
数学奥赛暑假天天练南京大学出版社系列答案科目：初中数学 来源： 题型：
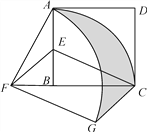
【题目】如图，在正方形ABCD中，AD＝2，E是AB的中点，将△BEC绕点B逆时针旋转90°后，点E落在CB的延长线上点F处，点C落在点A处．再将线段AF绕点F顺时针旋转90°得线段FG，连结EF、CG.
(1)求证：EF∥CG；
(2)求点C、点A在旋转过程中形成的
、
与线段CG所围成的阴影部分的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知正方形ABCD的边长为6，E，F分别是AB、BC边上的点，且∠EDF=45°，将△DAE绕点D逆时针旋转90°，得到△DCM．
(1)求证：EF=MF；
(2)若AE=2，求FC的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB，BC是⊙O的弦，∠B=60°，点O在∠B内，点D为
上的动点，点M，N，P分别是AD，DC，CB的中点．若⊙O的半径为2，则PN+MN的长度的最大值是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，梯形ABCD中，AB∥CD，∠ABC=90°，AB=8，CD=6，BC=4，AB边上有一动点P(不与A、B重合)，连结DP，作PQ⊥DP，使得PQ交射线BC于点E，设AP=x．
⑴当x为何值时，△APD是等腰三角形?
⑵若设BE=y，求y关于x的函数关系式；
⑶若BC的长可以变化，在现在的条件下，是否存在点P，使得PQ经过点C?若存在，求出相应的AP的长；若不存在，请说明理由，并直接写出当BC的长在什么范围内时，可以存在这样的点P，使得PQ经过点C．
查看答案和解析>>
科目：初中数学 来源： 题型：
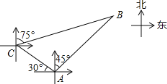
【题目】如图，甲、乙两只捕捞船同时在上午
从
港出海捕鱼．甲船以
的速度沿西偏北
方向前进，乙船以
的速度沿东北方向前进．甲船在
航行到达
处，此时甲船发现部分渔具丢在乙船上，于是甲船快速(匀速)沿北偏东
的方向追赶，结果两船在
处相遇．(其他因素不作考虑)
问乙船在什么时候被甲船追上；
求甲船追赶乙船的速度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（12分）如图所示是隧道的截面由抛物线和长方形构成，长方形的长是12 m，宽是4 m．按照图中所示的直角坐标系，抛物线可以用y=
x2+bx+c表示，且抛物线上的点C到OB的水平距离为3 m，到地面OA的距离为
m.
（1）求抛物线的函数关系式，并计算出拱顶D到地面OA的距离；
（2）一辆货运汽车载一长方体集装箱后高为6m，宽为4m，如果隧道内设双向车道，那么这辆货车能否安全通过？
（3）在抛物线型拱壁上需要安装两排灯，使它们离地面的高度相等，如果灯离地面的高度不超过8m，那么两排灯的水平距离最小是多少米？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数y=ax2+bx+c，自变量x与函数y的对应值如表：
下列说法正确的是（ ）
A. 抛物线的开口向下
B. 当x＞-3时，y随x的增大而增大
C. 二次函数的最小值是-2
D. 抛物线的对称轴是x=-
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com