
分析 (1)令x=0,求得y即可求得与y轴的交点;令y=0,求得x即可求得与x轴的交点;
(2)分成B是直角顶点,A是直角顶点以及P是直角顶点,利用全等三角形的性质以及相似三角形的性质即可求解;
(3)利用待定系数法求得直线CD的解析式,则C和D的坐标即可求得,然后根据S四边形ABCD=S△OCD-S△OAB求解.
解答 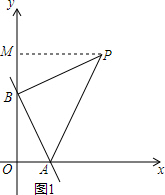 解:(1)在y=-2x+4中,令x=0,则y=4,则B的坐标是(0,4).
解:(1)在y=-2x+4中,令x=0,则y=4,则B的坐标是(0,4).
令y=0,则-2x+4=0,解得:x=2,则A的坐标是(2,0);
(2)当B是等腰△ABP的直角顶点时,如图1,作PM⊥y轴于点M.
∵∠PBA=90°,
∴∠PBM+∠ABO=90°,
又∵直角△BPM中,∠PBM+∠MPB=90°,
∴∠MPB=∠ABO,
在直角△BPM和直角△ABO中,
$\left\{\begin{array}{l}{∠MPB=∠ABP}\\{∠AOB=∠BMP}\\{AB=PB}\end{array}\right.$,
∴△BPM≌△ABO,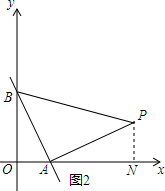
∴PM=OB=4,OA=BM=2.
∴OC=4+2,
∴P的坐标是(4,6);
当A是等腰△ABP的直角顶点时,如图2.
作PN⊥x轴于点N.同理可得△ABO≌△PAN,
∴PN=OA=2,AN=OB=4,
∴P的坐标是(6,2).
当P是直角三角形的直角顶点时,如图3.
作PF⊥y轴,交AB于点G,作PE⊥AB于点E,则PF∥x轴.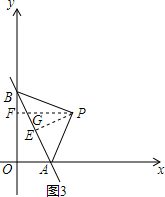 AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
PE=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{5}$=$\sqrt{5}$.
∵PF∥x轴,
∴∠PGE=∠OAB,
又∵∠PEG=∠AOB,
∴△OAB∽△EGP,
∴$\frac{PE}{OB}$=$\frac{PG}{AB}$=$\frac{EG}{OA}$,
∴$\frac{\sqrt{5}}{4}$=$\frac{PG}{2\sqrt{5}}$=$\frac{EG}{2}$,
解得:PG=$\frac{5}{2}$,EG=$\frac{\sqrt{5}}{2}$.
∴BG=$\frac{\sqrt{5}}{2}$,
∵PF∥x轴,
∴△BFG∽△BOA,
∴$\frac{BF}{OB}$=$\frac{BG}{AB}$=$\frac{FG}{OA}$,即$\frac{BF}{4}$=$\frac{\frac{\sqrt{5}}{2}}{2\sqrt{5}}$=$\frac{GF}{2}$,
∴BF=1,GF=$\frac{1}{2}$,
∴OF=4-1=3,PF=PG+FG=$\frac{5}{2}$+$\frac{1}{2}$=3,
∴P的坐标是(3,3);
(3)当如图1时,设经过P与AB平行的直线的解析式是y=-2x+b,则-4+b=6,
解得:b=10.
则直线的解析式是y=-2x+10.
令x=0,解得y=10;令y=0,解得x=5,则D的坐标是(0,10),C的坐标是(5,0).
则S四边形ABCD=S△OCD-S△OAB=$\frac{1}{2}$×5×10-$\frac{1}{2}$×2×4=21;
同理,P在图2的位置时,S=45;
当P的位置如图3时,S=$\frac{55}{4}$.
点评 本题考查了待定系数法求函数的解析式,以及等腰三角形的讨论求解,正确求得P的坐标是关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
 园艺师从土地上收集了许多大理石的边角料,准备给公共绿地的通道铺地面,其中最多的一种边角材料形状如图所示,你能否用这种边角料铺满地面?如果能,请设计出至少两种方案.
园艺师从土地上收集了许多大理石的边角料,准备给公共绿地的通道铺地面,其中最多的一种边角材料形状如图所示,你能否用这种边角料铺满地面?如果能,请设计出至少两种方案.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
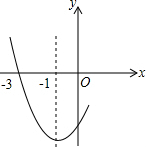 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0,④a+b+c=0.其中说法正确的是( )| A. | ①② | B. | ①②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com