
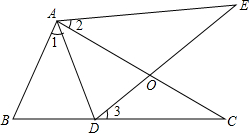
 如图,∠1=∠2=∠3,AB=AD,请说明BC=DE.
如图,∠1=∠2=∠3,AB=AD,请说明BC=DE.  名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
| 金额(元/人) | 20 | 30 | 40 | 50 | 60 |
| 学生数(人) | 3 | 17 | 5 | 12 | 3 |
| A. | 30 | B. | 40 | C. | 35 | D. | 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
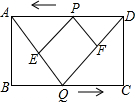 如图,矩形ABCD的边长AB=2cm,BC=5cm,两动点P、Q分别同时从点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过点P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
如图,矩形ABCD的边长AB=2cm,BC=5cm,两动点P、Q分别同时从点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过点P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
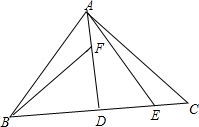 如图,在Rt△BAC中,已知AB=AC,∠BAC=90°,AD⊥BC于点D,点F、E分别在AD、DC上,且AF=CE,连接BF、AE.
如图,在Rt△BAC中,已知AB=AC,∠BAC=90°,AD⊥BC于点D,点F、E分别在AD、DC上,且AF=CE,连接BF、AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
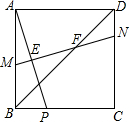 在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.
在正方形ABCD中,点P是边BC上一动点(不包含端点),线段AP的垂直平分线与AB、AP、BD、CD分别交于点M、E、F、N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
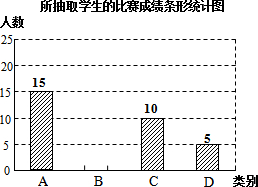 为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表:
为了提高学生写好汉字的积极性,某校组织全校学生参加汉字听写比赛,比赛成绩从高到低只分A、B、C、D四个等级.若随机抽取该校部分学生的比赛成绩进行统计分析,并绘制了如下的统计图表:| 成绩等级 | A | B | C | D |
| 人数 | 15 | x | 10 | 5 |
| 抽查学生占抽查 总数的百分比 | m | 40% | 20% | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM的长是( )
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M,N在边OB上,PM=PN,若MN=2,则OM的长是( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com