
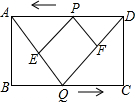
 如图,矩形ABCD的边长AB=2cm,BC=5cm,两动点P、Q分别同时从点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过点P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.
如图,矩形ABCD的边长AB=2cm,BC=5cm,两动点P、Q分别同时从点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过点P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F.分析 (1)根据ASA证得结论;
(2)①平行四边形PEQF为菱形,则PF=PE,根据全等三角形的性质来推知点P是AD的中点,易求其运动时间;
②由于四边形PEQF是矩形,那么∠EQF=90°,即∠AQB+∠DQC=90°,而∠AQB+∠QAB=90°,易得∠DQC=∠QAB,结合∠B=∠C=90°,易证△ABQ∽△QCD,进而得解.
解答 解:(1)∵点P是AD的中点,
∴AP=PD.
∵PE∥DQ,
∴∠APE=∠PDF,
∵PF∥AQ,
∴∠PAE=∠DPF,
∴在△APE与△PDF中,$\left\{\begin{array}{l}{∠APE=∠PDF}\\{AP=PD}\\{∠PAE=∠DPF}\end{array}\right.$,
∴△APE≌△PDF(ASA);
(2)∵PE∥DQ,PF∥AQ,
∴四边形PEQF是平行四边形
①当P,Q出发后 2.5s时,四边形PEQF为菱形,理由如下:
∵平行四边形PEQF是菱形,
∴PF=PE.
∵PE∥DQ,
∴∠APE=∠PDF,
∵PF∥AQ,
∴∠DPF=∠PAE,
∴△APE∽△PDF,
∴AP=PD,
∴PD=2.5cm,
∴t=2.5s;
(3)∵四边形PEQF是矩形,
∴∠EQF=90°,
∴∠AQB+∠DQC=90°,
又∵∠AQB+∠QAB=90°,
∴∠DQC=∠QAB,
∵∠B=∠C=90°,
∴△ABQ∽△QCD,
∴$\frac{AB}{CQ}$=$\frac{BQ}{DC}$,
设运动时间为t秒,则:BQ=5-t,则CQ=t,
即$\frac{2}{t}$=$\frac{5-t}{2}$,
∴t2-5t+4=0,
解得:t=1或t=4.
点评 本题考查了平行线的性质、相似三角形的判定和性质、等腰三角形三线合一定理、解一元二次方程、菱形性质、矩形性质,可先假设是菱形、矩形,再根据菱形、矩形的性质进行解答.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两条射线组成的图形叫做角 | |
| B. | 有公共端点的两条线段组成的图形叫做角 | |
| C. | 角可以看做是由一条射线绕着它的端点旋转而形成的图形 | |
| D. | 角可以看做是由一条线段绕着它的端点旋转而形成的图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 0.5 | C. | -5 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 太阳光强弱 | B. | 水的温度 | C. | 所晒时间 | D. | 热水器 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com