
| ���ְ�ģ�m2�� | ���ְ�ģ�m2�� | |
| A�� | 3 | 6 |
| B�� | 5 | 4 |
���� ��1����ÿ��A�ֿ�ʽ����������ΪaԪ��ÿ��B�ֿ�ʽ�Ҿߵ���������ΪbԪ����������1��A�ֿ�ʽ��2��B�ֿ�ʽ�ļҾߵ�����Ϊ1400Ԫ������2��A�ֿ�ʽ��3��B�ֿ�ʽ�Ҿߵ�����Ϊ2400Ԫ���г������飬���ɽ��
��2�����ȱ�ʾ��B���������������������ֿ�ʽ�Ҿ�ȫ������ʱ����������=A�����������+B��������������г���������ʽ��
����ȷ��x��ȡֵ��Χ���ٸ���һ�κ��������ʣ����ɽ��
��� �⣺��1����ÿ��A�ֿ�ʽ����������ΪaԪ��ÿ��B�ֿ�ʽ�Ҿߵ���������ΪbԪ��
��������ã�$\left\{\begin{array}{l}{a+2b=1400}\\{2a+3b=2400}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{a=600}\\{b=400}\end{array}\right.$��
��ÿ��A�ֿ�ʽ����������Ϊ600Ԫ��ÿ��B�ֿ�ʽ�Ҿߵ���������Ϊ400Ԫ��
��2����������ã�A����ȥ���а��3x��m2������B����ȥ���ְ��200-3x��m2����
��B��������$\frac{200-3x}{5}$�ף�
��������y=600x+$\frac{200-3x}{5}��400$=360x+16000��
�ڡ��ְ��ǡ��ȫ�����꣬
��0��x��65��
�֡�$6x+\frac{200-3x}{5}��4��250$��
��ã�x��25��
��y��x�����������
�൱x=25ʱ���ɻ���������
�������=360��25+16000=25000��Ԫ����
���� ���⿼�������һ�κ������ʵ�����⣬�������ǽ����п��е��ȵ����⣮ע������һ�κ�������ֵʱ���ؼ���Ӧ��һ�κ��������ʣ����ɺ���y��x�ı仯������Ա�����ȡֵ��Χȷ����ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��a2-b2����a+b����b-a�� | B�� | ��a2-b2����a+b�� | C�� | ��a2-b2����b-a�� | D�� | a2-b2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
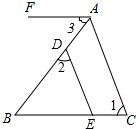 ��ͼ����D��E�ֱ���AB��BC�ϣ�DE��AC��AF��BC����1=70�㣬��2=55�㣬���3�Ķ����ǣ�������
��ͼ����D��E�ֱ���AB��BC�ϣ�DE��AC��AF��BC����1=70�㣬��2=55�㣬���3�Ķ����ǣ�������| A�� | 50�� | B�� | 53�� | C�� | 55�� | D�� | 58�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
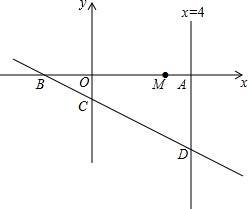 ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{1}{2}$x-1��x���y��ֱ���B��C���㣬��ֱ��x=4���ڵ�D��ֱ��x=4��x�ύ�ڵ�A����M��3��0������EΪֱ��x=4��һ���㣬��FΪֱ��y=-$\frac{1}{2}$x-1��һ���㣬ME+EF��СֵΪ$\frac{7\sqrt{5}}{5}$����ʱ��F������Ϊ��$\frac{18}{5}$��-$\frac{14}{5}$����
ƽ��ֱ������ϵ�У�ֱ��y=-$\frac{1}{2}$x-1��x���y��ֱ���B��C���㣬��ֱ��x=4���ڵ�D��ֱ��x=4��x�ύ�ڵ�A����M��3��0������EΪֱ��x=4��һ���㣬��FΪֱ��y=-$\frac{1}{2}$x-1��һ���㣬ME+EF��СֵΪ$\frac{7\sqrt{5}}{5}$����ʱ��F������Ϊ��$\frac{18}{5}$��-$\frac{14}{5}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
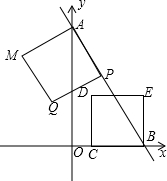 ��ͼ��ֱ��y=-$\frac{4}{3}$x+4�������ύ��A��B���㣬����P��C��1����λÿ����ͬ���ٶ�ͬʱ�ֱ�������AB��BO�����˶�����AP��BCΪ�߷ֱ�����ͼ������������APQM��BCDE���趯��P���˶�ʱ��Ϊt����������APQM�Ķ���Q����������BCDE�ı����ڵ�ֱ����ʱ��t��ֵΪ$\frac{5}{3}$��$\frac{15}{4}$��$\frac{20}{7}$��
��ͼ��ֱ��y=-$\frac{4}{3}$x+4�������ύ��A��B���㣬����P��C��1����λÿ����ͬ���ٶ�ͬʱ�ֱ�������AB��BO�����˶�����AP��BCΪ�߷ֱ�����ͼ������������APQM��BCDE���趯��P���˶�ʱ��Ϊt����������APQM�Ķ���Q����������BCDE�ı����ڵ�ֱ����ʱ��t��ֵΪ$\frac{5}{3}$��$\frac{15}{4}$��$\frac{20}{7}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com