
【题目】在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;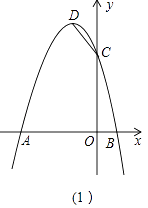
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.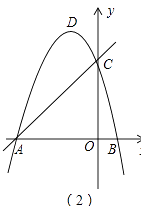
【答案】
(1)
解:当y=﹣x2﹣2x+3中y=0时,有﹣x2﹣2x+3=0,
解得:x1=﹣3,x2=1,
∵A在B的左侧,
∴A(﹣3,0),B(1,0).
当y=﹣x2﹣2x+3中x=0时,则y=3,
∴C(0,3).
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴顶点D(﹣1,4)
(2)
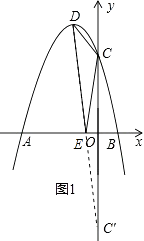
解:作点C关于x轴对称的点C′,连接C′D交x轴于点E,此时△CDE的周长最小,如图1所示.
∵C(0,3),
∴C′(0,﹣3).
设直线C′D的解析式为y=kx+b,
则有 ![]() ,解得:
,解得: ![]() ,
,
∴直线C′D的解析式为y=﹣7x﹣3,
当y=﹣7x﹣3中y=0时,x=﹣ ![]() ,
,
∴当△CDE的周长最小,点E的坐标为(﹣ ![]() ,0)
,0)
(3)
解:设直线AC的解析式为y=ax+c,
则有 ![]() ,解得:
,解得: ![]() ,
,
∴直线AC的解析式为y=x+3.
假设存在,设点F(m,m+3),
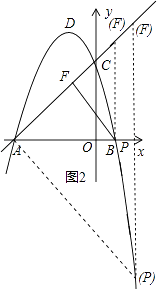
△AFP为等腰直角三角形分三种情况(如图2所示):
①当∠PAF=90°时,P(m,﹣m﹣3),
∵点P在抛物线y=﹣x2﹣2x+3上,
∴﹣m﹣3=﹣m2﹣2m+3,
解得:m1=﹣3(舍去),m2=2,
此时点P的坐标为(2,﹣5);
②当∠AFP=90°时,P(2m+3,0)
∵点P在抛物线y=﹣x2﹣2x+3上,
∴0=﹣(2m+3)2﹣2×(2m+3)+3,
解得:m3=﹣3(舍去),m4=﹣1,
此时点P的坐标为(1,0);
③当∠APF=90°时,P(m,0),
∵点P在抛物线y=﹣x2﹣2x+3上,
∴0=﹣m2﹣2m+3,
解得:m5=﹣3(舍去),m6=1,
此时点P的坐标为(1,0).
综上可知:在抛物线上存在点P,使得△AFP为等腰直角三角形,点P的坐标为(2,﹣5)或(1,0).
【解析】(1)令抛物线解析式中y=0,解关于x的一元二次方程即可得出点A、B的坐标,再令抛物线解析式中x=0求出y值即可得出点C坐标,利用配方法将抛物线解析式配方即可找出顶点D的坐标;(2)作点C关于x轴对称的点C′,连接C′D交x轴于点E,此时△CDE的周长最小,由点C的坐标可找出点C′的坐标,根据点C′、D的坐标利用待定系数法即可求出直线C′D的解析式,令其y=0求出x值,即可得出点E的坐标;(3)根据点A、C的坐标利用待定系数法求出直线AC的解析式,假设存在,设点F(m,m+3),分∠PAF=90°、∠AFP=90°和∠APF=90°三种情况考虑.根据等腰直角三角形的性质结合点A、F点的坐标找出点P的坐标,将其代入抛物线解析式中即可得出关于m的一元二次方程,解方程求出m值,再代入点P坐标中即可得出结论.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】甲乙两人在同一条道路上同时出发,同时行进,甲步行,乙骑车,出发时甲在前,乙在后,图中l甲,l乙,分别表示出发后甲、乙离出发地的路程s(km)和经历的时间t(h)的关系.

(1)乙出发时甲、乙相距___km.
(2)乙骑行一段路后,自行车发生故障,进行修理,所用的时间是___h.
(3)图象l甲,l乙相交的实际意义是什么?
(4)若乙的自行车没有故障,保持出发时的速度前进,求甲,乙相遇的时间和地点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,全球淡水资源日益减少,提倡全社会节约用水.据测试:拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小康同学洗手后,没有把水龙头拧紧,水龙头以测试的速度滴水,当小康离开x分钟后,水龙头滴出y毫升的水,请写出y与x之间的函数关系式是( )
A、y=0.05xB、y=5x
C、y=100xD、y=0.05x+100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D. 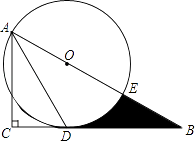
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC=3,∠B=30°.
①求⊙O的半径;
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块呈平行四边形的菜地,被分割成3个菱形和2个平行四边形后仍是中心对称图形.若只知道原平行四边形菜地的周长,则不用测量就能知道分割后的图形的周长的图形标号为( )
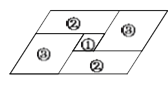
A. ①②③ B. ①② C. ②③ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,过点C作⊙O的切线交AB的延长线于点D,已知∠D=30°. 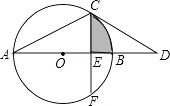
(1)求∠A的度数;
(2)若点F在⊙O上,CF⊥AB,垂足为E,CF= ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海边立有两座灯塔A、B,暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内,∠AOB=80°.为了避免触礁,轮船P与A、B的张角∠APB的最大值为 . 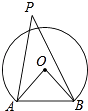
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com