
【题目】如图,一块呈平行四边形的菜地,被分割成3个菱形和2个平行四边形后仍是中心对称图形.若只知道原平行四边形菜地的周长,则不用测量就能知道分割后的图形的周长的图形标号为( )
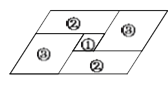
A. ①②③ B. ①② C. ②③ D. ①③
【答案】C
【解析】如图,
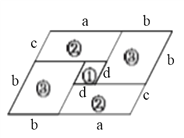
设图形②的长和宽分别是a、c,图形③的边长是b,图形①的边长是d,原来大平行四边形的周长是![]() ,
,
∵原来该大平行四边形的周长是![]() ,
,
∴2(a+2b+c)= ![]() .
.
根据图示,可得![]() ,
,
①②,可得:ab=bc,
∴2b=a+c,
∴![]() =2(a+2b+c)=2×2(a+c)=4(a+c),或
=2(a+2b+c)=2×2(a+c)=4(a+c),或![]() =2(a+2b+c)=2×4b=8b,
=2(a+2b+c)=2×4b=8b,
∴2(a+c)= ![]() ,4b=
,4b=![]() ,
,
∵图形③的周长是2(a+c),图形②的周长是4b,
∴图形①②的周长是定值,不用测量就能知道,图形①的周长不用测量无法知道。
∴分割后不用测量就能知道周长的图形的标号为②③。
故选:C.
点睛:此题主要考查了中心对称的性质和应用,要熟练掌握,解答此题的关键是要明确中心对称的性质: ①关于中心对称的两个图形能够完全重合; ②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为直线x=﹣1,且过点(﹣3,0),下列说法:①abc<0;②2a﹣b=0;③4a+2b+c<0;④若(﹣5,y1),(2.5,y2)是抛物线上两点,则y1>y2 , 其中说法正确的是( ) 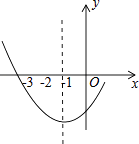
A.①②③
B.②③
C.①②④
D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=﹣x2﹣2x+3与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;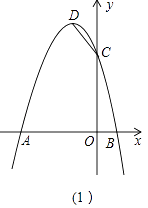
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.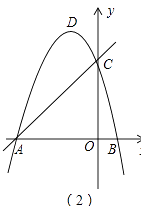
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习“锐角三角函数”中发现,用折纸的方法可求出tan22.5°,方法如下:将如图所示的矩形纸片ABCD沿过点B的直线折叠,使点A落在BC上的点E处,还原后,再沿过点E的直线折叠,使点A落在BC上的点F处,这样就可以知道tan22.5°= 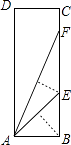
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校部分学生选择社团的意向,并将调查结果绘制成如下统计图(不完整):
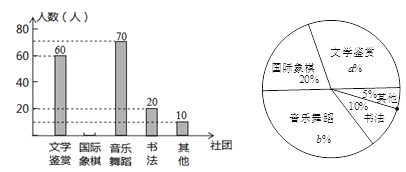
根据统计图的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为切实减轻中小学生课业负担、全面实施素质教育,某中学对本校学生课业负担情况进行调查.在本校随机抽取若干名学生进行问卷调查,发现被抽查的学生中,每天完成课外作业时间,最长不足120分钟,没有低于40分钟的,且完成课外作业时间低于60分钟的学生数占被调查人数的10%.现将抽查结果绘制成了一个不完整的频数分布直方图,如图所示. 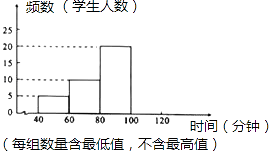
(1)这次被抽查的学生有人;
(2)请补全频数分布直方图;
(3)被调查这些学生每天完成课外作业时间的中位数在组(填时间范围);
(4)若该校共有3600名学生,请估计该校大约有多少名学生每天完成课外作业时间在80分钟以上(包括80分钟).
查看答案和解析>>
科目:初中数学 来源: 题型:
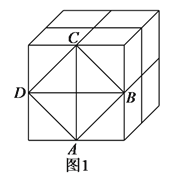
【题目】如图1,这是由8个同样大小的立方体组成的魔方,体积为64.
(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形![]() ,求出阴影部分的面积及其边长.
,求出阴影部分的面积及其边长.
(3)把正方形![]() 放到数轴上,如图
放到数轴上,如图![]() ,使得
,使得![]() 与
与![]() 重合,点
重合,点![]() 与
与![]() 重合,点
重合,点![]() 与点
与点![]() 关于
关于![]() 点对称,那么
点对称,那么![]() 在数轴上表示的数为__________;点
在数轴上表示的数为__________;点![]() 在数轴上表示的数为__________.
在数轴上表示的数为__________.
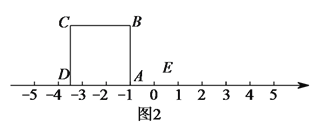
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点M在y轴的左侧,且在x轴的上侧,到两坐标轴的距离都是1,则点M的坐标为( )
A. (-1,2)B. (-1,-1)C. (-1,1)D. (1,1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com