
 如图,直线AB,CD交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的角平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB-2∠EOF,其中正确的结论有①③④(把所有正确结论的序号都填在横线上)
如图,直线AB,CD交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的角平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB-2∠EOF,其中正确的结论有①③④(把所有正确结论的序号都填在横线上) 分析 根据同角的余角相等可得∠AOF=∠DOE,即可判断①;根据角平分线的定义,无法证明OD为∠EOG的角平分线,即可判断②;根据角平分线的定义,可得∠BOD=∠BOG,由对顶角相等得出∠BOD=∠AOC,利用同角的余角相等可得∠BOD=∠EOF,即可判断③;根据平角的定义以及∠EOF=∠BOG=∠AOC,即可判断④.
解答 解:①∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∵∠DOF=90°,
∴∠AOE=∠DOF=90°,
∴∠AOF=∠DOE,
∴当∠AOF=60°时,∠DOE=60°,故①正确;
②∵不能证明∠GOD=∠EOD,
∴无法证明OD为∠EOG的角平分线,故②错误;
③∵OB平分∠DOG,
∴∠BOD=∠BOG.
∵直线AB,CD交于点O,
∴∠BOD=∠AOC.
∵∠BOE=∠DOF=90°,
∴∠BOD=∠EOF,
∴与∠BOD相等的角有三个,故③正确;
④∵∠COG=∠AOB-∠AOC-∠BOG,
∠EOF=∠BOG=∠AOC=∠BOD,
∴∠COG=∠AOB-2∠EOF,故④正确;
所以正确的结论有①③④.
故答案为①③④.
点评 本题考查了垂线,余角、对顶角以及角平分线的性质,注意结合图形,发现角与角之间的关系,难度适中.


科目:初中数学 来源: 题型:填空题
 如图,在3×3的正方形网格中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的概率是$\frac{5}{7}$.
如图,在3×3的正方形网格中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的概率是$\frac{5}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
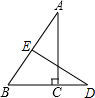 如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )
如图所示,在Rt△ABC中,∠ACB=90°,∠BAC=30°,BC=3cm,AB的垂直平分线DE交BC的延长线于点D,则CD的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com