
分析 先由中位数的概念求得x的值,再根据平均数和方差的计算公式进行计算即可.
解答 解:∵共有6个数据,排序后1总在中间,中位数应该是排序后的第3个数和第4个数的平均数,有$\frac{1}{2}$(x+1)=0,
∴x=-1,
数据的平均数=$\frac{1}{6}$(-3-2-1+5+6+1)=1,
∴$\frac{1}{6}$[(-3-1)2+(-2-1)2+(-1-1)2+(5-1)2+(1-1)2+(6-1)2]=$\frac{35}{3}$;
故答案为:$\frac{35}{3}$.
点评 本题考查方差和中位数,一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2];中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数).


科目:初中数学 来源: 题型:解答题
 本商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).
本商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费100元以上(不包括100元),就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准打折区域顾客就可以获得此项待遇(转盘等分成8份,指针停在每个区域的机会相等).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,直线AB,CD交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的角平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB-2∠EOF,其中正确的结论有①③④(把所有正确结论的序号都填在横线上)
如图,直线AB,CD交于点O,OE⊥AB,∠DOF=90°,OB平分∠DOG,给出下列结论:①当∠AOF=60°时,∠DOE=60°;②OD为∠EOG的角平分线;③与∠BOD相等的角有三个;④∠COG=∠AOB-2∠EOF,其中正确的结论有①③④(把所有正确结论的序号都填在横线上)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1.7 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
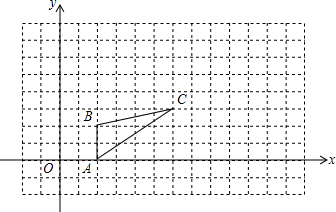 如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).
如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com