
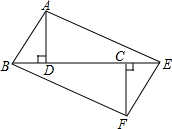
 如图,已知Rt△ABD≌Rt△FEC,且B、D、C、E在同一直线上,连接BF、AE.
如图,已知Rt△ABD≌Rt△FEC,且B、D、C、E在同一直线上,连接BF、AE.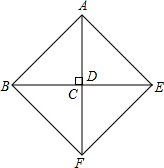 解:(1)∵Rt△ABD≌Rt△FEC,
解:(1)∵Rt△ABD≌Rt△FEC,

科目:初中数学 来源: 题型:
| A、打开电视机,屏幕上正在播放天气预报 |
| B、在地球上,抛出去的篮球会下落 |
| C、到电影院任意买一张电影票,座位号是奇数 |
| D、掷一枚均匀的骰子,向上一面的点数为偶数 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
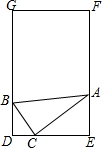 刘敏将一个直角三角板如图放置在一门框内,使得三角板的三个顶点恰好落在门框的三个边上,且点B距门框底端内缘0.4m,其中∠BAC=30°,∠ACB=90°,∠ACE=37°.
刘敏将一个直角三角板如图放置在一门框内,使得三角板的三个顶点恰好落在门框的三个边上,且点B距门框底端内缘0.4m,其中∠BAC=30°,∠ACB=90°,∠ACE=37°.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com