
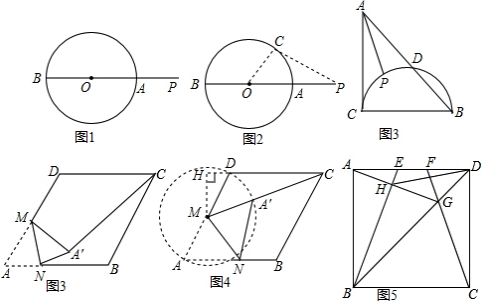
分析 探究:在⊙O上任取一点C(不为点A、B),连接PC、OC,证得PA<PC即可得到PA是点P到⊙O上的点的最短距离;
图中有圆,直接运用:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可;
图中无圆,构造运用:根据题意得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可;
迁移拓展,深化运用:根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△ADG和△CDG全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH=$\frac{1}{2}$AB=1,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.
解答 解:探究:
如图2,在⊙O上任取一点C(不为点A、B),连接PC、OC.
∵PO<PC+OC,PO=PA+OA,OA=OC,
∴PA<PC,
∴PA是点P到⊙O上的点的最短距离.(3分)
图中有圆,直接运用: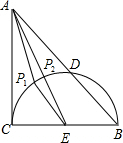 解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,P2E=1,
∴AP2=$\sqrt{5}$-1.
故答案为:$\sqrt{5}$-1;
图中无圆,构造运用:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FD=$\frac{1}{2}$MD=$\frac{1}{2}$,
∴FM=DM×cos30°=$\frac{\sqrt{3}}{2}$,
∴MC=$\sqrt{F{M}^{2}+C{F}^{2}}$=$\sqrt{7}$,
∴A′C=MC-MA′=$\sqrt{7}$-1.
故答案为:$\sqrt{7}$-1.
迁移拓展,深化运用:解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
$\left\{\begin{array}{l}{AB=CD}\\{∠BAD=∠CDA}\\{AE=DF}\end{array}\right.$,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADG=∠CDG}\\{DG=DG}\end{array}\right.$,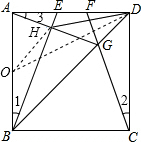
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°-90°=90°,
取AB的中点O,连接OH、OD,
则OH=AO=$\frac{1}{2}$AB=1,
在Rt△AOD中,OD=$\sqrt{A{O}^{2}+A{D}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
最小值=OD-OH=$\sqrt{5}$-1.
点评 本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,三角形的三边关系及圆的性质,确定出DH最小时点H的位置是解题关键,也是本题的难点.


科目:初中数学 来源: 题型:解答题
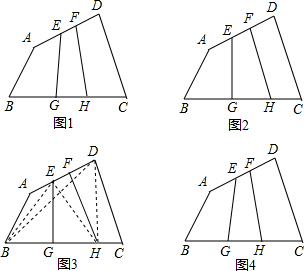 【提出问题】如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?
【提出问题】如图①,在四边形ABCD中,点E、F是AD的n等分点中最中间2个,点G、H是BC的n等分点中最中间2个,(其中n为奇数),连接EG、FH,那么S四边形EFHG与S四边形ABCD之间有什么关系呢?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
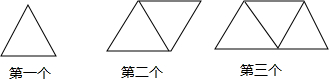
| 正三角形个数 | 1 | 2 | 3 | 4 | … | n |
| 火柴棒根数 | 3 | 5 | 7 | 9 | … | 2n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
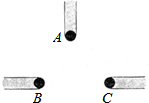 (1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?
(1)如图是小刚(A)、小明(B)、小勇(C)和他们各自影子的俯视图,他们所构成三角形地形的内部有一盏路灯,你认为如图是在白天阳光下的俯视图还是在晚上这盏路灯下的俯视图?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
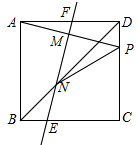 如图,正方形ABCD中,点P为CD上一点,线段AP的垂直平分线MN交BD于点N,点M为垂足,交两边于点E、F,连接PN,则下列结论,其中正确的有( )
如图,正方形ABCD中,点P为CD上一点,线段AP的垂直平分线MN交BD于点N,点M为垂足,交两边于点E、F,连接PN,则下列结论,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| x | … | -3 | -2 | -1 | 1 | 2 | 3 | … |
| y=-x+1 | … | 4 | 3 | 2 | 0 | -1 | -2 | … |
| y=-$\frac{2}{x}$ | … | $\frac{2}{3}$ | 1 | 2 | -2 | -1 | -$\frac{2}{3}$ | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com