
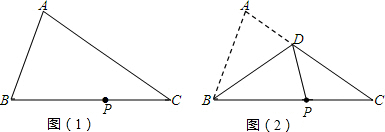
���� ��1������ƽ�ƹ��ɿ������ƽ�ƺ������ߵĽ���ʽ�����ø���ϵ���Ĺ�ϵ��AB�ij��ȣ���AB���ϵĸߣ����Ը��������ε������ʽ���Եõ�����m�ķ��̣�ͨ���ⷽ������m��ֵ��
��2������ƽ���ߵ����ʵõ���M��ֱ��PM�������ߵĽ��㣬��BC��PM�����Ը���ֱ���������ߵĽ�������н�ɣ�
��� 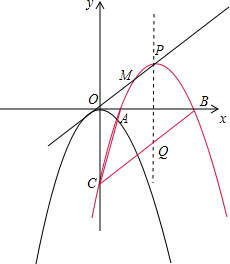 �⣺��1����A��x1��y1����B��x2��y2����
�⣺��1����A��x1��y1����B��x2��y2����
������y=-x2�Ķ��������ǣ�0��0����ƽ�ƺ������ߵĶ��������ǣ�m��n������ƽ�ƺ������ߵĽ���ʽΪ��
y=-��x-m��2+n��
�ߵ�n=2ʱ���������ߵĽ���ʽΪ��y=-��x-m��2+2=-x2+2mx-m2+2��
��x1+x2=2m��x1•x2=m2+2��OC=m2-2��
��AB=$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}•{x}_{2}}$=$\sqrt{4{m}^{2}-4��{m}^{2}-2��}$=2$\sqrt{2}$��
�ߡ�ABC�����Ϊ2$\sqrt{2}$��
��$\frac{1}{2}$AB•OC=$\frac{1}{2}$��2$\sqrt{2}$����m2-2��=2$\sqrt{2}$����m=2����ȥ��ֵ����
��2���ѵ�B������Ϊ��m+1��0��������y=-��x-m��2+n���ɵ�n=1��
�ߡ�MBC���PBC�������ȣ���M��ֱ��BC���Ϸ������������ϣ�
��BC��PM��
�ɣ�1���ɵ�P��m��n������Q��m��-n����
����P��m��1������Q��m��-1����
��ֱ��BQΪy=kx+b��k��0������
$\left\{\begin{array}{l}{0=k��m+1��+b}\\{-1=mk+b}\end{array}\right.$��
��� $\left\{\begin{array}{l}{k=1}\\{b=-��m+1��}\end{array}\right.$��
��ֱ��BQ�Ľ���ʽΪ��y=x-1��m+1����
����ֱ��MP�Ľ���ʽΪ��y=x+t��
��P��m��1�����룬��
1=m+t��
��� t=m-1��
��ֱ��MP�Ľ���ʽΪ��y=x+m-1��
������� $\left\{\begin{array}{l}{y=x+m-1}\\{y=-{x}^{2}+2mx-{m}^{2}+2}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=\frac{2m-1+\sqrt{13-8m}}{2}}\\{y=\frac{4m-3+\sqrt{13-8m}}{2}}\end{array}\right.$����M��$\frac{2m-1+\sqrt{13-8m}}{2}$��$\frac{4m-3+\sqrt{13-8m}}{2}$����
���� ���⿼���˶��κ���ͼ��ļ��α任��Ҫ��ѧ�������÷�������������������Ľ������ꡢ����������ֱ�ߵĽ������꣮


 ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д�
ȫ�ſ��䵥Ԫ�����������ܸ�ϰϵ�д� Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | 1 | 2 | 3 | �� |
| ͼ�� |  |  |  | �� |
| ��ĸ��� | 8 | 16 | 24 | �� |
| ��ĸ��� | 1 | 4 | 9 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
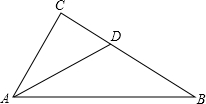 ��ͼ����������ABC�У���C=90�ȣ�AD�ǽ�ƽ���ߣ�CD=1.5��BD=2.5����AC�ij���
��ͼ����������ABC�У���C=90�ȣ�AD�ǽ�ƽ���ߣ�CD=1.5��BD=2.5����AC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
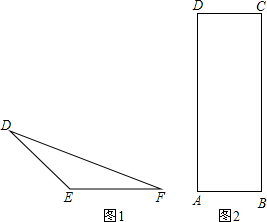 ��ͼ���ڵ���������DEF�У�DE=FE=1����DEF=135�㣮
��ͼ���ڵ���������DEF�У�DE=FE=1����DEF=135�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��2 | B�� | 5��3 | C�� | 8��5 | D�� | 13��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=7����O��BC�ϣ���CO=1����M��AC��һ���㣬����OM�����߶�OM�Ƶ�O��ʱ����ת90�㣬�õ��߶�OD��Ҫʹ��Dǡ������AB�ϣ�CM�ij���Ϊ5��
��ͼ���ڵ���Rt��ABC�У���C=90�㣬AC=7����O��BC�ϣ���CO=1����M��AC��һ���㣬����OM�����߶�OM�Ƶ�O��ʱ����ת90�㣬�õ��߶�OD��Ҫʹ��Dǡ������AB�ϣ�CM�ij���Ϊ5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com