
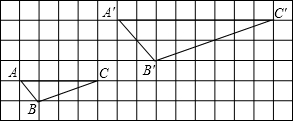
分析 设小正方形网格的边长为1,先计算出AB=$\sqrt{2}$,BC=$\sqrt{10}$,AC=4,A′B′=2$\sqrt{2}$,B′C′=2$\sqrt{10}$,A′C′=8,再得到∠C=∠C′,∠A=∠A′=45°,则可利用三种方法证明△ABC与△A′B′C′相似.
解答 解:△ABC与△A′B′C′相似.
设小正方形网格的边长为1,
证法(1)∵AB=$\sqrt{2}$,BC=$\sqrt{10}$,AC=4,A′B′=2$\sqrt{2}$,B′C′=2$\sqrt{10}$,A′C′=8,
∴$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$=$\frac{AC}{A′C′}$=$\frac{1}{2}$,
∴△ABC∽△A′B′C′;
证法(2)∵∠A=∠A′=45°,$\frac{AB}{A′B′}$=$\frac{BC}{B′C′}$,
∴△ABC∽△A′B′C′;
证法(3):∵tanC=$\frac{1}{3}$,tanC′=$\frac{2}{6}$=$\frac{1}{3}$,
∴∠C=∠C′,
∵∠A=∠A′=45°,
∴△ABC∽△A′B′C′.
点评 本题考查了相似三角形的判定:三组对应边的比相等的两个三角形相似;两边及其夹角法两组对应边的比相等且夹角对应相等的两个三角形相似;有两组角对应相等的两个三角形相似.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
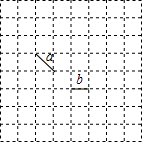 如图是8×8的格点,线段a、b的端点在格点上,请在图中画出第三条线段,使其端点在格点上且与线段a、b组成轴对称图形.(画出所有情况,并在图中把这些线段标记为线段c、d、e、f、g….)
如图是8×8的格点,线段a、b的端点在格点上,请在图中画出第三条线段,使其端点在格点上且与线段a、b组成轴对称图形.(画出所有情况,并在图中把这些线段标记为线段c、d、e、f、g….)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
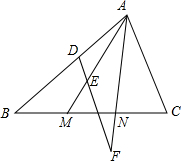 如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求$\frac{EF}{DE}$的值.
如图,已知M、N为△ABC的边BC上的两点,且满足BM=MN=NC,一条平行于AC的直线分别交AB、AM和AN的延长线于点D、E和F,求$\frac{EF}{DE}$的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
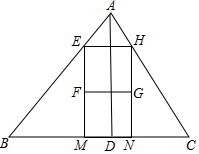 在△ABC中,已知边BC=12,该边上的高线AD=8,同样大小的两个正方形FMNG与EFGH按如图所示方式叠放,其中顶点M、N在BC边上,E、H分别在AB、AC上,求正方形的边长.
在△ABC中,已知边BC=12,该边上的高线AD=8,同样大小的两个正方形FMNG与EFGH按如图所示方式叠放,其中顶点M、N在BC边上,E、H分别在AB、AC上,求正方形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com