
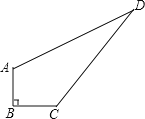
【题目】为将我们的城市装扮的更美丽,园林绿化工人要将公园一角的一块四边形的空地ABCD种植上花草.经测量,∠B=90°,AB=3米,BC=4米,CD=12米,DA=13米.若每平方米空地需要购买150元的花草.将这块空地全部绿化需要购买多少元的这种花草?
【答案】这块空地全部绿化需要购买5400元的这种花草.
【解析】
连接AC,在直角三角形ABC中可求得AC的长,由AC、CD、AD的长度关系可得三角形DAC为直角三角形,DA为斜边;由此看,四边形ABCD由Rt△ABC和Rt△DAC构成,则容易求解.
连接AC,
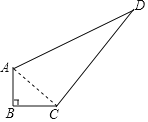
在Rt△ABC中,AC2=AB2+BC2=32+42=52,
在△CAD中,AD2=132,DC2=122,
而122+52=132,
即AC2+CD2=AD2,
∴∠DCA=90°,
S四边形ABCD=S△BAC+S△DAC=![]() BCAB+
BCAB+![]() DCAC,
DCAC,
=![]() ×4×3+
×4×3+![]() ×12×5=36,
×12×5=36,
所以需费用36×150=5400(元),
答:这块空地全部绿化需要购买5400元的这种花草.


科目:初中数学 来源: 题型:
【题目】问题背景
在数学活动课上,张老师要求同学们拿两张大小不同的矩形纸片进行旋转变换探究活动.如图 1,在矩形纸片ABCD 和矩形纸片EFGH中,AB=1,AD=2,且FE>AD,FG>AB,点E 是 AD 的中点,矩形纸片 EFGH 以点E 为旋转中心进行逆时针旋转,在旋转过程中会产生怎样的数量关系,提出恰当的数学问题并加以解决.
解决问题
下面是三个学习小组提出的数学问题,请你解决这些问题.
(1)“奋进”小组提出的问题是:如图 1,当 EF 与 AB 相交于点 M,EH 与 BC 相交于点 N 时,求证:EM=EN.
(2)“雄鹰”小组提出的问题是:在(1)的条件下,当 AM=CN 时,AM 与 BM 有怎样的数量关系,请说明理由.
(3)“创新”小组提出的问题是:若矩形 EFGH 继续以点 E 为旋转中心进行逆时针旋转,当 ![]() 时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.
时,请你在图 2 中画出旋转后的示意图,并求出此时 EF 将边 BC 分成的两条线段的长度.


查看答案和解析>>
科目:初中数学 来源: 题型:
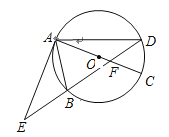
【题目】如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,AF=4,CF=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校一班级开展为贫困山区学生捐钱助学活动,该班有20名学生捐出了自己的零花钱,捐款数如下:(单位:元)
19 | 20 | 25 | 30 | 28 | 27 | 26 | 21 | 20 | 22 | 24 | 23 | 25 | 29 | 27 | 28 | 27 | 30 | 19 | 20 |
该班老师准备将此次活动的捐款数据制成频数分布直方图,在制图时请你帮老师算出以下数据:
(1)计算最大值与最小值的差;
(2)若选定组距为2计算将这20个数据分成的组数;并计算将第一组的起点定为18.5时捐款数在26.5-28.5范围内的频数;
(3)计算第一组和最后一组这两个组内包含的所有样本的平均数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小方格都是边长为1的正方形,已知学校的坐标为A(2,2).
(1)请在图中建立适当的直角坐标系,并写出图书馆的坐标;
(2)若体育馆的坐标为C(-2,3),请在坐标系中标出体育馆的位置,并顺次连接学校、图书馆、体育馆,得到△ABC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
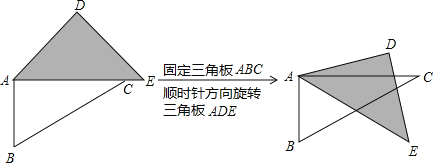
【题目】如图1,将三角板ABC与三角板ADE摆放在一起;如图2,固定三角板ABC,将三角板ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).当△ADE的一边与△ABC的某一边平行(不共线)时,写出旋转角α的所有可能的度数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
(2)写出∠DON的余角.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批LED灯泡与普通白炽灯炮,其进价与标价如下表,该商场购进LED灯泡与普通白炽灯炮共300个,LED灯泡按标价进行销售,而普通白炽灯炮按标价打九折销售,销售完这批灯泡后可以获利3200元。
(1)求该商场购进LED灯泡与普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进两种灯泡120个,并在不打折的情况下销售完,若销售完这批灯泡的获利不超过总进货价的28%,则最多购进LED灯泡多少个?
LED灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求S△COB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com