
【题目】如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上. 
(1)填空:∠ABC= , BC=;
(2)判断△ABC与△DEF是否相似?并证明你的结论.
【答案】
(1)135°;2 ![]()
(2)解:△ABC∽△DEF.
证明:∵在4×4的正方形方格中,
∠ABC=135°,∠DEF=90°+45°=135°,
∴∠ABC=∠DEF.
∵AB=2,BC=2 ![]() ,FE=2,DE=
,FE=2,DE= ![]()
∴ ![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]() =
= ![]() .
.
∴△ABC∽△DEF
【解析】(1)解:∠ABC=90°+45°=135°, BC= ![]() =
= ![]() =2
=2 ![]() ;
;
故答案为:135°;2 ![]() .
.
(1)根据已知条件,结合网格可以求出∠ABC的度数,根据,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上,利用勾股定理即可求出线段BC的长;(2)根据相似三角形的判定定理,夹角相等,对应边成比例即可证明△ABC与△DEF相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】探究题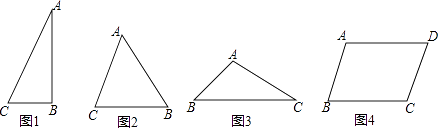
【问题提出】
已知任意三角形的两边及夹角(是锐角),求三角形的面积.
【问题探究】
为了解决上述问题,让我们从特殊到一般展开探究.
探究:在Rt△ABC(图1)中,∠ABC=90°,AC=b,BC=a,∠C=α,求△ABC的面积(用含a、b、α的代数式表示)
在Rt△ABC中,∠ABC=90°
∴sinα= ![]()
∴AB=bsinα
∴S△ABC= ![]() BCAB=
BCAB= ![]() absinα
absinα
(1)探究一:
锐角△ABC(图2)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
(2)探究二:
钝角△ABC(图3)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
(3)【问题解决】
用文字叙述:已知任意三角形的两边及夹角(是锐角),求三角形面积的方法
是
(4)已知平行四边形ABCD(图4)中,AB=b,BC=a,∠B=α(0°<α<90°)
求:平行四边形ABCD的面积.(用含a、b、α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题
问题再现:
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性,从而可以帮助我们快速解题.初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
例如:利用图形的几何意义证明完全平方公式.
证明:将一个边长为a的正方形的边长增加b,形成两个矩形和两个正方形,如图1: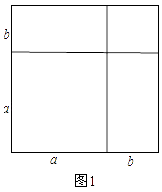
这个图形的面积可以表示成:
(a+b)2或a2+2ab+b2
∴(a+b)2 =a2+2ab+b2
这就验证了两数和的完全平方公式.
(1)类比解决:
请你类比上述方法,利用图形的几何意义证明平方差公式.(要求画出图形并写出推理过程)
(2)问题提出:如何利用图形几何意义的方法证明:13+23=32?
如图2,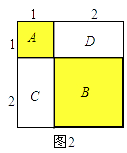
A表示1个1×1的正方形,即:1×1×1=13
B表示1个2×2的正方形,C与D恰好可以拼成1个2×2的正方形,因此:B、C、D就可以表示2个2×2的正方形,即:2×2×2=23
而A、B、C、D恰好可以拼成一个(1+2)×(1+2)的大正方形.
由此可得:13+23=(1+2)2=32
尝试解决:
请你类比上述推导过程,利用图形的几何意义确定:13+23+33= . (要求写出结论并构造图形写出推证过程).
(3)问题拓广:
请用上面的表示几何图形面积的方法探究:13+23+33+…+n3= . (直接写出结论即可,不必写出解题过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象解决下列问题:
(1)分别求出y甲,y乙与x的函数关系式;
(2)现厂家分配该商品给甲、乙两商场共计1200件,当甲、乙商场售完这批商品,厂家可获得总利润为1080元,问厂家如何分配这批商品?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
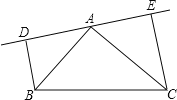
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.
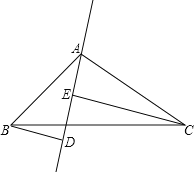
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC. 
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OP过Rt△ABC的边AC、AB的中点M、N,AC=4cm,BC=4 ![]() cm,OM=3cm.射线OP上有一动点Q从点O出发,沿射线OP以每秒1cm的速度向右移动,以Q为圆心,QM为半径的圆,经过t秒与BC、AB中的一边所在的直线相切,请写出t的所有可能值(单位:秒)
cm,OM=3cm.射线OP上有一动点Q从点O出发,沿射线OP以每秒1cm的速度向右移动,以Q为圆心,QM为半径的圆,经过t秒与BC、AB中的一边所在的直线相切,请写出t的所有可能值(单位:秒) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)![]()
(2)(2x)2x4÷x
(3)![]()
(4)![]()
(5)(x﹣2)(2+x)﹣(2﹣x)(x﹣2)
(6)(6x4y2+8x3y4)÷2xy2﹣(﹣2xy)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com