
【题目】探究题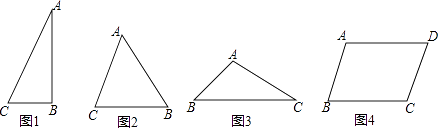
【问题提出】
已知任意三角形的两边及夹角(是锐角),求三角形的面积.
【问题探究】
为了解决上述问题,让我们从特殊到一般展开探究.
探究:在Rt△ABC(图1)中,∠ABC=90°,AC=b,BC=a,∠C=α,求△ABC的面积(用含a、b、α的代数式表示)
在Rt△ABC中,∠ABC=90°
∴sinα= ![]()
∴AB=bsinα
∴S△ABC= ![]() BCAB=
BCAB= ![]() absinα
absinα
(1)探究一:
锐角△ABC(图2)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
(2)探究二:
钝角△ABC(图3)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
(3)【问题解决】
用文字叙述:已知任意三角形的两边及夹角(是锐角),求三角形面积的方法
是
(4)已知平行四边形ABCD(图4)中,AB=b,BC=a,∠B=α(0°<α<90°)
求:平行四边形ABCD的面积.(用含a、b、α的代数式表示)
【答案】
(1)
如图2中,作AH⊥CB于H.
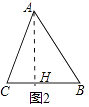
在Rt△AHC中,∠AHC=90°
∴sinα= ![]()
∴AH=bsinα
∴S△ABC= ![]() BCAH=
BCAH= ![]() absinα
absinα
(2)
如图3中,作AH⊥CB于H.
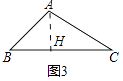
在Rt△AHC中,∠AHC=90°
∴sinα= ![]() ,
,
∴AH=bsinα
∴S△ABC= ![]() BCAH=
BCAH= ![]() absinα
absinα
(3)S= ![]() absin∠C(∠C是a、b两边的夹角)
absin∠C(∠C是a、b两边的夹角)
(4)
如图4中,作AH⊥CB于H.
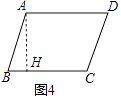
在Rt△AHB中,∠AHB=90°
∴sinα= ![]() ,
,
∴AH=bsinα
∴S平行四边形ABCD=BCAH=absinα.
【解析】探究二:如图2中,作AH⊥CB于H.求出高AH,即可解决问题;探究三:如图3中,作AH⊥CB于H.求出高AH,即可解决问题;
问题解决:S= ![]() absin∠C(∠C是a、b两边的夹角);问题应用:如图4中,作AH⊥CB于H.求出高AH,即可解决问题;
absin∠C(∠C是a、b两边的夹角);问题应用:如图4中,作AH⊥CB于H.求出高AH,即可解决问题;
【考点精析】关于本题考查的三角形的“三线”和三角形的面积,需要了解1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;三角形的面积=1/2×底×高才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,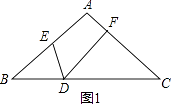
求证:DECD=DFBE
(2)D为BC中点如图2,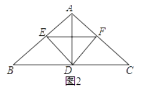
连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知四边形ABCD的四条边相等,四个内角都等于90°,点E是CD边上一点,F是BC边上一点,且∠EAF=45°.
(1)求证:BF+DE=EF;
(2)若AB=6,设BF=x,DE=y,求y关于x的函数解析式,并写出x的取值范围;
(3)过点A作AH⊥FE于点H,如图(2),当FH=2,EH=1时,求△AFE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交与点P,BE与CD交于点Q,连接PQ.
求证:(1)AD=BE
(2)△APC≌△BQC
(3)△PCQ是等边三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在4×4的正方形方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上. 
(1)填空:∠ABC= , BC=;
(2)判断△ABC与△DEF是否相似?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com