
【题目】如图(1),已知四边形ABCD的四条边相等,四个内角都等于90°,点E是CD边上一点,F是BC边上一点,且∠EAF=45°.
(1)求证:BF+DE=EF;
(2)若AB=6,设BF=x,DE=y,求y关于x的函数解析式,并写出x的取值范围;
(3)过点A作AH⊥FE于点H,如图(2),当FH=2,EH=1时,求△AFE的面积.

【答案】(1)见解析;(2)y=![]() (0≤x≤6);(3)
(0≤x≤6);(3)![]() .
.
【解析】
(1)如图1中,将△ADE绕点A顺时针旋转90°得到△ABH.只要证明△AFH≌△AFE(SAS)即可解决问题;,
(2)利用(1)中结论,在Rt△ECF中,根据EF2=CF2+EC2,构建关系式即可;
(3)如图2中,将△ADE绕点A顺时针旋转90°得到△ABM.首先证明AH=AB,设AB=x,在Rt△EFC中,利用勾股定理构建方程即可解决问题;
(1)如图1中,将△ADE绕点A顺时针旋转90°得到△ABH,
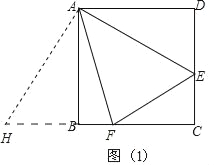
∵四边形ABCD是正方形,
∴AB=AD=CD=BC,∠BAD=90°,
∵∠EAF=45°,
∴∠BAF+∠BAH=∠BAF+∠DAE=45°,
∴∠FAH=∠FAE=45°,
∵AF=AF,AH=AE,
∴△AFH≌△AFE(SAS),
∴EF=FH,
∵FH=BH+BF=DE+BF,
∴EF=BF+DE;
(2)∵AB=BC=CD=6,BF=x,DE=y,
∴EF=x+y,FC=6=﹣x,EC=6﹣y,
在Rt△ECF中,∵EF2=CF2+EC2,
∴(x+y)2=(6﹣x)2+(6﹣y)2,
∴y=![]() (0≤x≤6);
(0≤x≤6);
(3)如图2中,将△ADE绕点A顺时针旋转90°得到△ABM.
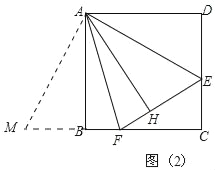
由(1)可知△AFM≌△AFH,
∵AB⊥FM,AH⊥EF,
∴AB=AH,
设AB=BC=CD=AD=x,
∵∠ABF=∠AHF=90°,
∵AF=AF.AB=AH,
∴Rt△AFB≌Rt△AFH(HL),
∴BF=FH=2,同理可证:DE=EH=1,
∴CF=x﹣2,EC=x﹣1,
在Rt△ECF中,∵EF2=CF2+EC2,
∴32=(x﹣2)2+(x﹣1)2,
∴x=![]() 或
或![]() (舍弃),
(舍弃),
∴S△AEF=![]() EFAH=
EFAH=![]() ×3×
×3×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】为了了解某学校初四年级学生每周平均课外阅读时间的情况,随机抽查了该学校初四年级m名同学,对其每周平均课外阅读时间进行统计,绘制了如下条形统计图(图一)和扇形统计图(图二):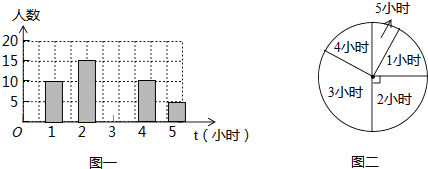
(1)根据以上信息回答下列问题:
①求m值.
②求扇形统计图中阅读时间为5小时的扇形圆心角的度数.
③补全条形统计图.
(2)直接写出这组数据的众数、中位数,求出这组数据的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 AB,CD 相交于点O,OE 平分∠AOD,OF⊥OC.
(1)图中∠AOF 的余角是_____ _____(把符合条件的角都填出来);
(2)如果∠AOC=120°,那么根据____ ______,可得∠BOD=__________°;
(3)如果∠1=32°,求∠2和∠3的度数.
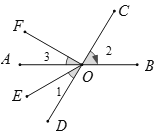
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,∠B=15°,边AB的垂直平分线交边BC于点E,垂足为点D,取线段BE的中点F,联结DF.求证:AC=DF.(说明:此题的证明过程需要批注理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃. 
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究题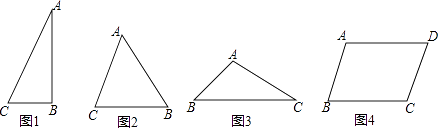
【问题提出】
已知任意三角形的两边及夹角(是锐角),求三角形的面积.
【问题探究】
为了解决上述问题,让我们从特殊到一般展开探究.
探究:在Rt△ABC(图1)中,∠ABC=90°,AC=b,BC=a,∠C=α,求△ABC的面积(用含a、b、α的代数式表示)
在Rt△ABC中,∠ABC=90°
∴sinα= ![]()
∴AB=bsinα
∴S△ABC= ![]() BCAB=
BCAB= ![]() absinα
absinα
(1)探究一:
锐角△ABC(图2)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
(2)探究二:
钝角△ABC(图3)中,AC=b,BC=a,∠C=α(0°<α<90°)
求:△ABC的面积.(用含a、b、α的代数式表示)
(3)【问题解决】
用文字叙述:已知任意三角形的两边及夹角(是锐角),求三角形面积的方法
是
(4)已知平行四边形ABCD(图4)中,AB=b,BC=a,∠B=α(0°<α<90°)
求:平行四边形ABCD的面积.(用含a、b、α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某商场有甲、乙两种商品,甲种每件进价15元,售价20元;乙种每件进价35元,售价45元.
(1)若商家同时购进甲、乙两种商品100件,设甲商品购进x件,售完此两种商品总利润为y 元.写出y与x的函数关系式.
(2)该商家计划最多投入3000元用于购进此两种商品共100件,则至少要购进多少件甲种商品?若售完这些商品,商家可获得的最大利润是多少元?
(3)“五一”期间,商家对甲、乙两种商品进行表中的优惠活动,小王到该商场一次性付款324元购买此类商品,商家可获得的最小利润和最大利润各是多少?
打折前一次性购物总金额 | 优惠措施 |
不超过400元 | 售价打九折 |
超过400元 | 售价打八折 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com