
【题目】如图,已知Rt△ABC中,∠ACB=90°,∠B=15°,边AB的垂直平分线交边BC于点E,垂足为点D,取线段BE的中点F,联结DF.求证:AC=DF.(说明:此题的证明过程需要批注理由)

【答案】见解析
【解析】
先根据线段垂直平分线的性质得:AE=BE,再利用直角三角形斜边中线的性质得:DF与BE的关系,最后根据直角三角形30度的性质得AC和AE的关系,从而得出结论.
连接AE,
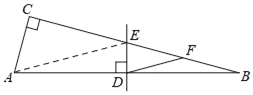
∵DE是AB的垂直平分线(已知),
∴AE=BE,∠EDB=90°(线段垂直平分线的性质),
∴∠EAB=∠EBA=15°(等边对等角),
∴∠AEC=30°(三角形的一个外角等于与它不相邻的两个内角的和),
Rt△EDB中,∵F是BE的中点(已知),
∴DF=![]() BE(直角三角形斜边中线等于斜边的一半),
BE(直角三角形斜边中线等于斜边的一半),
Rt△ACE中,∵∠AEC=30°(已知),
∴AC=![]() AE(直角三角形30°角所对的直角边是斜边的一半),
AE(直角三角形30°角所对的直角边是斜边的一半),
∴AC=DF(等量代换).


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AD∥BC,AB⊥BC,AB=3,点E为射线BC上一个动点,连接AE,将△ABE沿AE折叠,点B落在点B′处,过点B′作AD的垂线,分别交AD,BC于点M,N.当点B′为线段MN的三等分点时,BE的长为 . 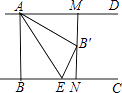
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC,点D、E、F分别在BC、AB、AC上,∠EDF=∠B.
(1)如图1,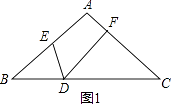
求证:DECD=DFBE
(2)D为BC中点如图2,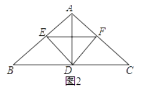
连接EF.
①求证:ED平分∠BEF;
②若四边形AEDF为菱形,求∠BAC的度数及 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知四边形ABCD的四条边相等,四个内角都等于90°,点E是CD边上一点,F是BC边上一点,且∠EAF=45°.
(1)求证:BF+DE=EF;
(2)若AB=6,设BF=x,DE=y,求y关于x的函数解析式,并写出x的取值范围;
(3)过点A作AH⊥FE于点H,如图(2),当FH=2,EH=1时,求△AFE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=DB,∠1=∠2,请问添加下面哪个条件不能判断△ABC≌△DBE的是( )

A. BC=BE B. ∠A=∠D C. ∠ACB=∠DEB D. AC=DE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数y= ![]() 的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
的图象交于A(﹣2,m),B(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D. 
(1)求这两个函数的解析式:
(2)求△ADC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com