
����Ŀ��ij����������������Ҫ���Ĵ������ܣ�����ÿǧ�ȵ��������������һ�κ�����ϵ���������㣬����ÿǧ�ȵ��������y��Ԫ/ǧ�ȣ�������x��Ԫ/ǧ�ȣ��ĺ���ͼ����ͼ��
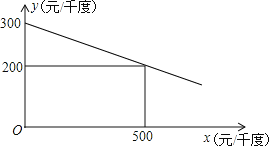
��1�������Ϊ600Ԫ/ǧ��ʱ����������ÿǧ�ȵ���������Ƕ��٣�
��2��Ϊ��ʵ�ֽ��ܼ���Ŀ�꣬�йز��Ź涨���ó����x��Ԫ/ǧ�ȣ���ÿ���õ���m��ǧ�ȣ��ĺ�����ϵΪx=10m+500���Ҹù���ÿ���õ���������60ǧ�ȣ�Ϊ�˻�����������ÿ��Ӧ����ʹ�ö��ٶȵ磿����ÿ�����ĵ������������Ƕ���Ԫ��
���𰸡���1����������ÿǧ�ȵ����������180Ԫ��2��������ÿ������50ǧ�ȵ�ʱ������ÿ�����ĵ��������Ϊ5000Ԫ
�������������������1����y=kx+b��k��0�������ô���ϵ������һ�κ�������ʽ��ɣ�
��2����������=ÿ����õ�����ÿǧ�ȵ��������y��Ȼ�������õ�W��m�Ĺ�ϵʽ���ٸ��ݶ��κ�������ֵ������
�⣺��1���蹤��ÿǧ�ȵ��������y��Ԫ/ǧ�ȣ�����x��Ԫ/ǧ�ȣ��ĺ�������ʽΪ��y=kx+b��
���ú���ͼ����㣨0��300������500��200����
��![]() ��
��
���![]() ��
��
����y=��0.2x+300��x��0����
�����x=600Ԫ/ǧ��ʱ���ù�������ÿǧ�ȵ��������y=��0.2��600+300=180��Ԫ/ǧ�ȣ���
��2���蹤��ÿ�����ĵ��������ΪwԪ��������ã�
w=my=m����0.2x+300��
=m[��0.2��5m+600��+300]
=��m2+180m
=����m��90��2+8100��
��m��90ʱ��w��m����������
�����⣬m��60��
����m=60ʱ��w���=����60��90��2+8100=7200��
��������ÿ������60ǧ�ȵ�ʱ������ÿ�����ĵ��������Ϊ����������Ϊ7200Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ף����70����������ij����С���A�س������ڶ�������Ĺ�·�ϼ���·����·������涨����ʻΪ����������ʻΪ����һ�����ߴ���ʻ��¼���£���λ��km��.

��1���չ�ʱ��A�صľ����� ��
��2���ڵ� �μ�¼ʱ��A����Զ.��������� km
��3����ÿkm����0.2���������ߴι����Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=��x+2��2+m��ͼ����y�ύ�ڵ�C����B���������ϣ������C���������ߵĶԳ���Գƣ���֪һ�κ���y=kx+b��ͼ���ö��κ���ͼ���ϵĵ�A����1��0������B��
��1������κ�����һ�κ����Ľ���ʽ��
��2������ͼ��д�����㣨x+2��2+m��kx+b��x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2��bx��c(a��0)��ͼ����ͼ��ʾ������ͼ�����������⣮
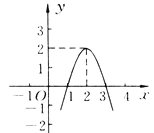
(1)�����ax2��bx��c��0����������
(2)д������ʽax2��bx��c��0�Ľ⼯��
(3)д��y��x���������С���Ա���x��ȡֵ��Χ��
(4)������ax2��bx��c��k����������ȵ�ʵ��������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
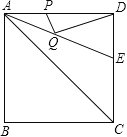
����Ŀ����ͼ��������ABCD�ı߳���2����DAC��ƽ���߽�DC�ڵ�E������P��Q�ֱ���AD��AE�ϵĶ��㣬��DQ+PQ����СֵΪ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������̽������֪��ֽ������һ����(��ͼ��ʾ)��
![]()
����һ��
(1)�۵�ֽ�棬ʹ1��ʾ�ĵ��룭1��ʾ�ĵ��غϣ���3��ʾ�ĵ���________��ʾ�ĵ��غϣ�
��������
(2)�۵�ֽ�棬ʹ��1��ʾ�ĵ���3��ʾ�ĵ��غϣ��ش��������⣺
��5��ʾ�ĵ�����________��ʾ�ĵ��غϣ�
����������A��B����֮�����Ϊ11(A��B�����)����A��B���㾭�۵����غϣ���A��B�����ʾ�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ǿ����ó�����ͬ�Ļ�����һ�����ɴ�����������ͼ����ͼ������8��������ͼ������15���������������˹��ɣ���n��ͼ����Ҫ________����������2 019��ͼ����Ҫ________��������
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���������������ϴ������е�A��B��C������AB=2��BC=1����ͼ��ʾ�����A��B��C����Ӧ���ĺ���p.
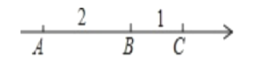
(1)����BΪԭ�㣬д����A��C����Ӧ������������p��ֵ������CΪԭ�㣬p���Ƕ���?
(2)��ԭ��O��ͼ�������ϵ�C���ұߣ���CO=28����p.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y��ax2��bx��c(a��0)��ͼ����ͼ��ʾ����|ax2��bx��c|��k(k��0)����������ȵ�ʵ��������k��ȡֵ��Χ��( )

A. k����3 B. k����3 C. k��3 D. k��3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com