【题目】如图，我们可以用长度相同的火柴棒按一定规律搭正多边形组成图案，图案①需8根火柴棒，图案②需15根火柴棒，…，按此规律，第n个图案需要________根火柴棒，第2 019个图案需要________根火柴棒．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，小河上有一拱桥，拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE，ED，DB组成，已知河底ED是水平的，ED＝16m，AE＝8m，抛物线的顶点C到ED的
距离是11m，以ED所在的直线为x轴，抛物线的对称轴为y轴建立平面直角坐标系．
(1)求抛物线的解析式；
(2)已知从某时刻开始的40h内，水面与河底ED的距离h(单位：m)随时间t(单位：h)的变化满足函数
关系
且当水面到顶点C的距离不大于5m时，需禁止船只通行，请通过计算说明：在这一时段内，需多少小时禁止船只通行？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】读一读：式子“1+2+3+4+5+…+100”表示1开始的100个连续自然数的和．由于上述式子比较长，书写也不方便，为了简便起见，我们可以将“1+2+3+4+5+…+100”表示为
，这里“
”是求和符号．例如：1+3+5+7+9+…+99，即从1开始的100以内的连续奇数的和，可表示为
（2n-1）；又如13+23+33+43+53+63+73+83+93+103可表示为
n3．
通过对上以材料的阅读，请解答下列问题．
（1）2+4+6+8+10+…+100（即从2开始的100以内的连续偶数的和）用求和符合可表示为_________________；
（2）计算
（n2-1）=________________．（填写最后的计算结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某工厂在生产过程中要消耗大量电能，消耗每千度电产生利润与电价是一次函数关系，经过测算，工厂每千度电产生利润y（元/千度））与电价x（元/千度）的函数图象如图：
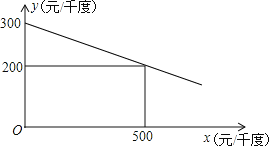
（1）当电价为600元/千度时，工厂消耗每千度电产生利润是多少？
（2）为了实现节能减排目标，有关部门规定，该厂电价x（元/千度）与每天用电量m（千度）的函数关系为x=10m+500，且该工厂每天用电量不超过60千度，为了获得最大利润，工厂每天应安排使用多少度电？工厂每天消耗电产生利润最大是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
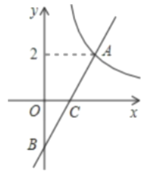
【题目】如图在平面直角坐标系
中，函数
的图象与一次函数
的图象的交点为
．
（1）求一次函数的解析式；
（2）设一次函数
的图象与
轴交于点
，若点
是
轴上一点，且满足
的面积是6，求点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点A、B、C、D、E在同一直线上，且AC＝BD，E是线段BC的中点．
（1）点E是线段AD的中点吗？说明理由；
（2）当AD＝10，AB＝3时，求线段BE的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】气象台发布的卫星云图显示,代号为
的台风在某海岛(设为点
)的南偏东
方向的
点生成,测得
.台风中心从点
以
的速度向正北方向移动，经
后到达海面上的点
处.因受气旋影响,台风中心从点
开始以
的速度向北偏西
方向继续移动.以
为原点建立如图所示的直角坐标系．
(1)台风中心生成点
的坐标为 ,台风中心转折点
的坐标为 ；(结果保留根号)
(2)已知距台风中心
范围内均会受到台风侵袭.如果某城市(设为点
)位于点
的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，O是坐标原点，点A的坐标是(－2，4)，过点A作AB⊥y轴，垂足为B，连接OA.
(1)求△OAB的面积；
(2)若抛物线y＝－x2－2x＋c经过点A.
①求c的值；
②将抛物线向下平移m个单位长度，使平移后得到的抛物线顶点落在△OAB的内部(不包括△OAB的边界)，求m的取值范围(直接写出答案即可)．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
