
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | $\frac{2+\sqrt{2}}{2}$ |
科目:初中数学 来源: 题型:解答题
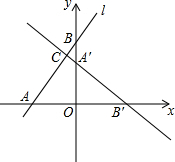 如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
如图,在平面直角坐标系中,直线l:y=$\frac{4}{3}$x+4分别交x轴、y轴于点A、B,将△AOB绕点O顺时针旋转90°后得到△A′OB′.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
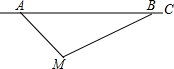 根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.
根据道路管理规定,在贺州某段笔直公路上行驶的车辆,限速40千米/时,已知交警测速点M到该公路A点的距离为10$\sqrt{2}$米,∠MAB=45°,∠MBA=30°(如图所示),现有一辆汽车由A往B方向匀速行驶,测得此车从A点行驶到B点所用的时间为3秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售单价x(元) | … | 230 | 235 | 240 | 245 | … |
| 销售量y(件) | … | 440 | 430 | 420 | 410 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
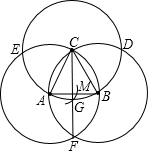 如图,分别以边长1为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,求AM的长.
如图,分别以边长1为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,求AM的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com