
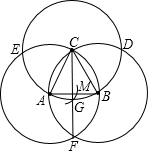
 如图,分别以边长1为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,求AM的长.
如图,分别以边长1为的等边三角形ABC的顶点为圆心,以其边长为半径作三个等圆,得交点D、E、F,连接CF交⊙C于点G,以点E为圆心,EG长为半径画弧,交边AB于点M,求AM的长. 分析 如图,过点E作EP⊥AB,连接EA、EC,易得△EAC为正三角形,△ABC为正三角形;由正三角形的性质、平行线的性质求得△ECG为等腰直角三角形,根据勾股定理、圆的半径的性质推知EM=EG=$\sqrt{2}$;然后在直角△EPA和直角△EPM中由勾股定理、线段间的和差关系求得AM的长度.
解答 解:如图,过点E作EP⊥AB,连接EA、EC、EM.
∵在⊙C中,EC=AC;在⊙A中,AE=AC,
∴EC=AC=AE,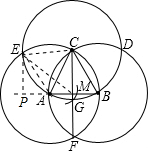
∴△EAC为正三角形;
同理证得△ABC为正三角形,则∠ECA=∠CAB=60°,
∴EC∥AB,
又∵由相交两圆的性质得:CG⊥AB,
∴EC⊥CG,
∴EM=EG=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∵∠EAP=60°,
∴EP=$\frac{\sqrt{3}}{2}$,AP=$\frac{1}{2}$,PM=$\sqrt{E{M}^{2}-E{P}^{2}}$=$\frac{\sqrt{5}}{2}$,
∴AM=PM-AP=$\frac{\sqrt{5}}{2}$-1.
点评 本题考查了圆的综合题.此题涉及到的知识点有:勾股定理、等边三角形的判定与性质以及线段间的和差关系,解题的关键是正确的作出题目的辅助线,题目难度较大,综合性较强.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{2}$ | B. | $\sqrt{2}$ | C. | 2-$\sqrt{2}$ | D. | $\frac{2+\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
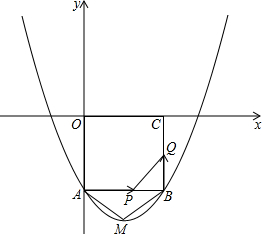 如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,最低点为M,且S△AMB=$\frac{5}{6}$
如图,在平面直角坐标系xOy中,正方形OABC的边长为2cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,最低点为M,且S△AMB=$\frac{5}{6}$查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com